Ciontú

Is é atá i gcomhréiteach feidhm chomhghaoil f (τ) leis an bhfeidhm aisiompaithe g (t-τ).

Is é siombail an réiltín * an t-oibreoir convolution .

Tá diongbháilteacht f (t) agus g (t) cothrom le slánuimhir f (τ) huaire f (t-τ):

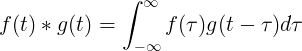
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

Sainmhínítear ciontú 2 fheidhm scoite mar:

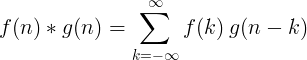
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

Úsáidtear convolution scoite déthoiseach de ghnáth le haghaidh próiseála íomhá.

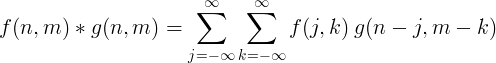
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

Is féidir linn an comhartha ionchuir scoite x (n) a scagadh trí luí leis an bhfreagra neamhchlaonta h (n) chun an comhartha aschuir y (n) a fháil.

y ( n ) = x ( n ) * h ( n )

Tá claochlú Fourier ar iolrú 2 fheidhm cothrom le diongbháilteacht na gclaochlú Fourier ar gach feidhm:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

Tá claochlú Fourier ar chiontú de 2 fheidhm cothrom le iolrú na gclaochlú Fourier ar gach feidhm:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Féach freisin