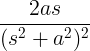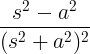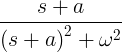Claochlú Laplace

Athraíonn Laplace translate feidhm fearainn ama go feidhm s-fearainn trí chomhtháthú ó nialas go héigríoch

den fheidhm fearainn ama, arna iolrú faoi e ^-st .

Úsáidtear an claochlú Laplace chun réitigh a fháil go tapa ar chothromóidí difreálacha agus ar shlánuimhreacha.

Déantar díorthú sa réimse ama a chlaochlú go iolrú faoi s sa bhfearann s.

Déantar comhtháthú sa réimse ama a athrú go deighilt de réir s sa bhfearann.

Feidhm claochlaithe Laplace

Sainmhínítear an claochlú Laplace leis an oibreoir L {}:

$F (í) = \ mathcal {L} \ ar chlé \ {f (t) \ deas \} = \ int_ {0} ^ {\ infty} e ^ {- st} f (t) dt$

Is féidir an claochlú Laplace inbhéartach a ríomh go díreach.

De ghnáth tugtar an claochlú inbhéartach ón tábla trasfhoirmithe.

Ainm feidhme	Feidhm fearainn ama	Claochlú Laplace
Ainm feidhme	f ( t )	F ( í ) = L { f ( t )}
Tairiseach	1	$\ frac {1} {s}$
Líneach	t	$\ frac {1} {s ^ 2}$
Cumhacht	t ⁿ	$\ frac {n!} {s ^ {n + 1}}$
Cumhacht	t ^a	Γ ( a +1) ⋅ s ^{- ( a +1)}
Taispeántóir	e ^ag	$\ frac {1} {sa}$
Sín	pheaca ag	$\ frac {a} {s ^ 2 + a ^ 2}$
Cosine	cos ag	$\ frac {s} {s ^ 2 + a ^ 2}$
Sine hipearbóileach	sinh ag	$\ frac {a} {s ^ 2-a ^ 2}$
Cosine hipearbóileach	cosh ag	$\ frac {s} {s ^ 2-a ^ 2}$
Fás sine	t sin ag	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Cosine ag fás	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Sin ag lobhadh	e ^-Ag sin ωt	$\ frac {\ omega} {\ chlé (s + a \ dheis) ^ 2 + \ omega ^ 2}$
Cosine ag lobhadh	e ^-Ag cos ωt	$\ frac {s + a} {\ chlé (s + a \ deas) ^ 2 + \ omega ^ 2}$
Feidhm Delta	δ ( t )	1
Moill delta	δ ( ta )	e ^-as

Ainm na maoine	Feidhm fearainn ama	Claochlú Laplace	Tráchtaireacht
	f ( t )	F ( í )
Línteacht	af ( t ) + bg ( t )	aF ( í ) + bG ( í )	a , b seasmhach
Athrú scála	f ( at )	$\ frac {1} {a} F \ chlé (\ frac {s} {a} \ ar dheis)$	a / 0
Aistriú	e ^-at f ( t )	F ( s + a )
Moill	f ( ta )	e ^{- mar} F ( í )
Díorthú	$\ frac {df (t)} {dt}$	sF ( í ) - f (0)
Díorthú N-ú	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( í ) - s ^{n -1}f (0) - s ^{n -2}f ’(0) -...- f ^{( n -1)} (0)
Cumhacht	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Comhtháthú	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (í)$
Cómhalartach	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ infty} F (x) dx$
Ciontú	f ( t ) * g ( t )	F ( í ) ⋅ G ( í )	* is é an t-oibreoir convolution
Feidhm thréimhsiúil	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$