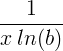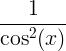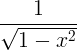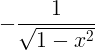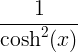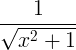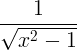Rialacha díorthacha

Rialacha agus dlíthe díorthacha. Tábla díorthach feidhmeanna.

Sainmhíniú díorthach

Is é díorthach feidhme an cóimheas idir an difríocht idir luach feidhme f (x) ag pointí x + Δx agus x le Δx, nuair a bhíonn Δx beag gan teorainn. Is é an díorthach fána feidhme nó fána na líne tadhlaí ag pointe x.

 

f '(x) = \ lim _ {\ Delta x \ to 0} \ frac {f (x + \ Delta x) -f (x)} {\ Delta x}

An dara díorthach

Tugtar an dara díorthach trí:

Nó faigh an chéad díorthach go simplí:

f '' (x) = (f '(x))'

Nú díorthach

Tá an n tá ú díorthach a ríomh trí chineann f (x) n amanna.

Tá an n ú díorthach cothrom le díorthach an díorthaigh (n-1):

f ( n ) ( x ) = [ f ( n -1) ( x )] '

Sampla:

Faigh an ceathrú díorthach de

f ( x ) = 2 x 5

f (4) ( x ) = [2 x 5 ] '' '' = [10 x 4 ] '' '= [40 x 3 ]' '= [120 x 2 ]' = 240 x

Díorthach ar ghraf na feidhme

Is é díorthach feidhme fána an líne inláimhsithe.

Rialacha díorthacha

Riail suim díorthach

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Riail táirge díorthach

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
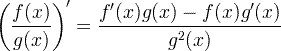Riail comhrann díorthach \ clé (\ frac {f (x)} {g (x)} \ deas) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}
Riail slabhra díorthach

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Riail suim díorthach

Nuair a bhíonn a agus b tairisigh.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Sampla:

Faigh an díorthach:

3 x 2 + 4 x.

De réir riail na suimeanna:

a = 3, b = 4

f ( x ) = x 2 , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x 2 + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Riail táirge díorthach

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Riail comhrann díorthach

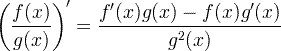
\ clé (\ frac {f (x)} {g (x)} \ deas) '= \ frac {f' (x) g (x) -f (x) g '(x)} {g ^ 2 ( x)}

Riail slabhra díorthach

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Is féidir an riail seo a thuiscint níos fearr le nodaireacht Lagrange:

\ frac {df} {dx} = \ frac {df} {dg} \ cdot \ frac {dg} {dx}

Comhfhogasú líneach feidhme

Maidir le Δx beag, is féidir linn comhfhogasú a fháil go f (x 0 + Δx), nuair a bhíonn f (x 0 ) agus f ’(x 0 ) ar eolas againn:

f ( x 0 + Δ x ) ≈ f ( x 0 ) + f '( x 0 ) ⋅Δ x

Tábla díorthach feidhmeanna

Ainm feidhme Feidhm Díorthach

f ( x )

 f '( x )
Tairiseach

const

0

Líneach

x

1

Cumhacht

x a

ax a- 1
Easpónantúil

e x

e x
Easpónantúil

a x

a x ln a
Logarithm nádúrtha

ln ( x )

Logarithm

log b ( x )

Sín

sin x

cos x
Cosine

cos x

-sin x
Tadhlaí

tan x

Arcsine

arcsin x

Arccosine

arccos x

Arctangent

arctan x
Sine hipearbóileach

sinh x

cosh x
Cosine hipearbóileach

cosh x

sinh x
Tadhlaí hipearbóileach

tanh x

Sinsearach hipearbóileach inbhéartach

sinh -1 x

Cosine hipearbóileach inbhéartach

cosh -1 x

Tadhlaí hipearbóileach inbhéartach

tanh -1 x

Samplaí díorthacha

Sampla # 1

f ( x ) = x 3 +5 x 2 + x +8

f ' ( x ) = 3 x 2 + 2⋅5 x + 1 + 0 = 3 x 2 +10 x +1

Sampla # 2

f ( x ) = sin (3 x 2 )

Agus an riail slabhra á chur i bhfeidhm:

f ' ( x ) = cos (3 x 2 ) ⋅ [3 x 2 ]' = cos (3 x 2 ) ⋅ 6 x

An dara tástáil dhíorthach

Nuair is nialas an chéad díorthach feidhme ag pointe x 0 .

f '( x 0 ) = 0

Ansin is féidir leis an dara díorthach ag pointe x 0 , f '' (x 0 ), cineál an phointe sin a léiriú:

 

f '' ( x 0 )/ 0

 íosmhéid áitiúil

f '' ( x 0 ) <0

 uasmhéid áitiúil

f '' ( x 0 ) = 0

 neamhchinntithe

 

Féach freisin

Advertising

CALCULUS
TÁBLAÍ RAPID