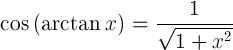Feidhm arctangent
Arctan (x), tan -1 (x), feidhm tadhlaí inbhéartaigh .
Sainmhíniú arctan
Sainmhínítear arctangent x mar fheidhm tadhlaí inbhéartaigh x nuair atá x fíor (x ∈ℝ ).
Nuair atá tadhlaí y cothrom le x:
tan y = x
Ansin tá an t-arctangent de x cothrom le feidhm tadhlaí inbhéartaigh x, atá cothrom le y:
arctan x = tan -1 x = y
Sampla
arctan 1 = tan -1 1 = π / 4 rad = 45 °
Graf arctan
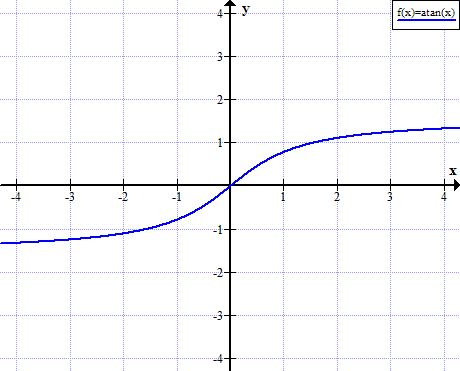
Rialacha Arctan
| Ainm na rialach | Riail |
|---|---|
| Tadhlaí arctangent |
tan (arctan x ) = x |
| Arctan argóint dhiúltach |
arctan (- x ) = - arctan x |
| Suim Arctan |
arctan α + arctan β = arctan [( α + β ) / (1- αβ )] |
| Difríocht Arctan |
arctan α - arctan β = arctan [( α - β ) / (1+ αβ )] |
| Sín arctangent |
|
| Cosine arctangent |
|
| Argóint chómhalartach |
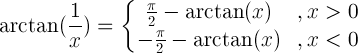 |
| Arctan ó arcsin |
|
| Díorthach arctan |
|
| Cuid dhílis éiginnte den arctan |
|
Tábla Arctan
| x | arctan (x) (rad) |
arctan (x) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1.2490 | -71.565 ° |
| -2 | -1.1071 | -63.435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0.5 | -0.4636 | -26.565 ° |
| 0 | 0 | 0 ° |
| 0.5 | 0.4636 | 26.565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63.435 ° |
| 3 | 1.2490 | 71.565 ° |
| ∞ | π / 2 | 90 ° |
Féach freisin
- Feidhm tadhlaí
- Feidhm arccosine
- Feidhm arcsine
- Arctan de 0
- Arctan de 1
- Arctan de 2
- Arctan an Infinity
- Díorthach arctan
- Comhtháite arctan
- Sín arctan
- Cosine arctan
- Graf Arctan
- Áireamhán Arctan
- Céimeanna go tiontaire raidianacha
Advertising
TRIGONOMETRY
TÁBLAÍ RAPID