Feidhm Arccos (x)
ARccOS (x), cos -1 (x), inbhéartach Comhshíneas fheidhm.
Sainmhíniú arccos
Tá arccosine na x shainmhíniú mar an inbhéartach Comhshíneas fheidhm x nuair -1≤x≤1.
Nuair a bhíonn cosine y cothrom le x:
cos y = x
Ansin tá an t-arccosine de x cothrom le feidhm chosain inbhéartach x, atá cothrom le y:
arccos x = cos -1 x = y
(Anseo ciallaíonn cos -1 x an cosine inbhéartach agus ní chiallaíonn sé cosine do chumhacht -1).
Sampla
arccos 1 = cos -1 1 = 0 rad = 0 °
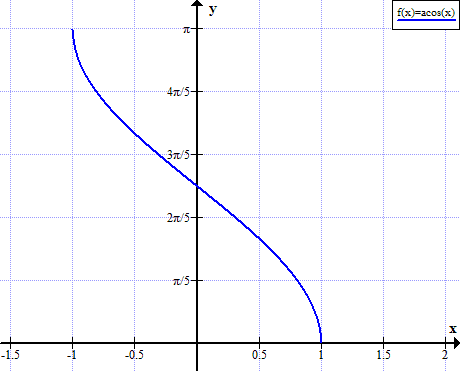
Graf na n-arccos
Rialacha Arccos
| Ainm na rialach | Riail |
|---|---|
| Cosain arccosine | cos (arccos x ) = x |
| Arccosine na cosine | arccos (cos x ) = x + 2 k π, nuair a bhíonn k ∈ℤ ( k slánuimhir) |
| Arccos argóint dhiúltach | arccos (- x ) = π - arccos x = 180 ° - arccos x |
| Uillinneacha comhlántacha | arccos x = π / 2 - arcsin x = 90 ° - arcsin x |
| Suim Arccos | arccos ( α ) + arccos ( β ) = arccos ( αβ - √ (1- α 2 ) (1- β 2 ) ) |
| Difríocht Arccos | arccos ( α ) - arccos ( β ) = arccos ( αβ + √ (1- α 2 ) (1- β 2 ) ) |
| Arccos pheaca x | arccos (sin x ) = - x - (2 k +0.5) π |
| Sín arccosine |
|
| Tadhlaí arccosine |
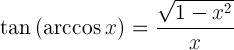 |
| Díorthach arccosine |
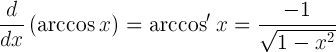 |
| Cuid dhílis éiginnte de arccosine |
|
Tábla Arccos
| x | arccos (x) (rad) |
arccos (x) (°) |
|---|---|---|
| -1 | π | 180 ° |
| -√ 3 /2 | 5π / 6 | 150 ° |
| -√ 2 /2 | 3π / 4 | 135 ° |
| -1/2 | 2π / 3 | 120 ° |
| 0 | π / 2 | 90 ° |
| 1/2 | π / 3 | 60 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 6 | 30 ° |
| 1 | 0 | 0 ° |
Féach freisin
- Feidhm cosine
- Feidhm arcsine
- Arctanfunction
- Áireamhán Arccos
- Tiontairí raidianacha go céimeanna
- Arccos de 0
- Arccos de 1
- Arccos de 2
- Arccos de 3
- Arccos de chos
- Arccos an pheaca
- Díorthach Arccos
- Graf Arccos
- Cos arccos
- Sin de arccos
- Tan de arccos
Advertising