ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ - ln (x)

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಎನ್ನುವುದು ಒಂದು ಸಂಖ್ಯೆಯ ಮೂಲ e ಗೆ ಲಾಗರಿಥಮ್ ಆಗಿದೆ.

• ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ (ಎಲ್ಎನ್) ವ್ಯಾಖ್ಯಾನ
• ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ (ಎಲ್ಎನ್) ನಿಯಮಗಳು ಮತ್ತು ಗುಣಲಕ್ಷಣಗಳು
  • ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ (ಎಲ್ಎನ್) ನ ವ್ಯುತ್ಪನ್ನ
  • ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್‌ನ ಸಮಗ್ರ (ln)
• ಸಂಕೀರ್ಣ ಲಾಗರಿಥಮ್
• Ln (x) ನ ಗ್ರಾಫ್
• ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ಸ್ (ಎಲ್ಎನ್) ಟೇಬಲ್
• ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕ್ಯಾಲ್ಕುಲೇಟರ್

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ನ ವ್ಯಾಖ್ಯಾನ

ಯಾವಾಗ

e ^y = x

ನಂತರ x ನ ಬೇಸ್ ಇ ಲಾಗರಿಥಮ್ ಆಗಿದೆ

ln ( x ) = ಲಾಗ್ _ಇ ( x ) = y

 

ಇ ನಿರಂತರ ಅಥವಾ ಯುಲರ್ ಸಂಖ್ಯೆ:

e ≈ 2.71828183

ಘಾತೀಯ ಕ್ರಿಯೆಯ ವಿಲೋಮ ಕ್ರಿಯೆಯಾಗಿ Ln

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕ್ರಿಯೆ ln (x) ಎನ್ನುವುದು ಘಾತೀಯ ಕ್ರಿಯೆಯ ವಿಲೋಮ ಕ್ರಿಯೆ e ^x .

X/ 0 ಗಾಗಿ,

f ( f ^-1 ( x )) = e ^{ln ( x )} = x

ಅಥವಾ

f ^-1 ( f ( x )) = ln ( e ^x ) = x

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ನಿಯಮಗಳು ಮತ್ತು ಗುಣಲಕ್ಷಣಗಳು

ನಿಯಮದ ಹೆಸರು	ನಿಯಮ	ಉದಾಹರಣೆ
ಉತ್ಪನ್ನ ನಿಯಮ	ln ( x ∙ y ) = ln ( x ) + ln ( y )	ln (3 ∙ 7) = ln (3) + ln (7)
ಪ್ರಮಾಣ ನಿಯಮ	ln ( x / y ) = ln ( x ) - ln ( y )	ಹಾಗೂ ln (3 / 7) = ಹಾಗೂ ln (3) - ಹಾಗೂ ln (7)
ವಿದ್ಯುತ್ ನಿಯಮ	ln ( x y ) = y ln ( x )	ಹಾಗೂ ln (2 8 ) = 8 ∙ ಹಾಗೂ ln (2)
ln ಉತ್ಪನ್ನ	f ( x ) = ln ( x ) ⇒ f ' ( x ) = 1 / x
ln ಅವಿಭಾಜ್ಯ	Ln ( x ) dx = x ∙ (ln ( x ) - 1) + C.
negative ಣಾತ್ಮಕ ಸಂಖ್ಯೆಯ ln	x ≤ 0 ಆಗ ln ( x ) ಅನ್ನು ವಿವರಿಸಲಾಗುವುದಿಲ್ಲ
ln ಶೂನ್ಯ	ln (0) ಅನ್ನು ವಿವರಿಸಲಾಗುವುದಿಲ್ಲ
ಒಂದು ln	ln (1) = 0
ln ಅನಂತ	ಲಿಮ್ ಹಾಗೂ ln ( ಕ್ಷ ) = ∞, ಆಗ ಕ್ಷ → ∞
ಯೂಲರ್ನ ಗುರುತು	ಹಾಗೂ ln (-1) = ನಾನು π

 

ಲಾಗರಿಥಮ್ ಉತ್ಪನ್ನ ನಿಯಮ

X ಮತ್ತು y ನ ಗುಣಾಕಾರದ ಲಾಗರಿಥಮ್ x ನ ಲಾಗರಿಥಮ್ ಮತ್ತು y ನ ಲಾಗರಿಥಮ್ನ ಮೊತ್ತವಾಗಿದೆ.

log _b ( x y ) = log _b ( x ) + log _b ( y )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ ₁₀ (3 ∙ 7) = ಲಾಗ್ ₁₀ (3) + ಲಾಗ್ ₁₀ (7)

ಲಾಗರಿಥಮ್ ಅಂಶ ನಿಯಮ

X ಮತ್ತು y ನ ವಿಭಜನೆಯ ಲಾಗರಿಥಮ್ x ನ ಲಾಗರಿಥಮ್ ಮತ್ತು y ನ ಲಾಗರಿಥಮ್ನ ವ್ಯತ್ಯಾಸವಾಗಿದೆ.

log _b ( x / y ) = log _b ( x ) - log _b ( y )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ ₁₀ (3 / 7) = ಲಾಗ್ ₁₀ (3) - ಲಾಗ್ ₁₀ (7)

ಲಾಗರಿಥಮ್ ವಿದ್ಯುತ್ ನಿಯಮ

Y ನ ಶಕ್ತಿಗೆ ಬೆಳೆದ x ನ ಲಾಗರಿಥಮ್ x ನ ಲಾಗರಿಥಮ್‌ನ y ಪಟ್ಟು.

log _b ( x ^y ) = y log _b ( x )

ಉದಾಹರಣೆಗೆ:

ಲಾಗ್ ₁₀ (2 ⁸ ) = 8 ∙ ಲಾಗ್ ₁₀ (2)

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್‌ನ ವ್ಯುತ್ಪನ್ನ

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕ್ರಿಯೆಯ ವ್ಯುತ್ಪನ್ನವು ಪರಸ್ಪರ ಕ್ರಿಯೆಯಾಗಿದೆ.

ಯಾವಾಗ

f ( x ) = ln ( x )

ಎಫ್ (ಎಕ್ಸ್) ನ ಉತ್ಪನ್ನ ಹೀಗಿದೆ:

f ' ( x ) = 1 / x

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್‌ನ ಸಮಗ್ರ

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕ್ರಿಯೆಯ ಅವಿಭಾಜ್ಯವನ್ನು ಇವರಿಂದ ನೀಡಲಾಗಿದೆ:

ಯಾವಾಗ

f ( x ) = ln ( x )

ಎಫ್ (ಎಕ್ಸ್) ನ ಅವಿಭಾಜ್ಯ:

∫ ಎಫ್ ( ಕ್ಷ ) dx ನ್ನು = ∫ ಹಾಗೂ ln ( ಕ್ಷ ) dx ನ್ನು = ಕ್ಷ ∙ (ಹಾಗೂ ln ( ಕ್ಷ ) - 1) + ಸಿ

0 ರ ಎಲ್ಎನ್

ಶೂನ್ಯದ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಅನ್ನು ವಿವರಿಸಲಾಗುವುದಿಲ್ಲ:

ln (0) ಅನ್ನು ವಿವರಿಸಲಾಗುವುದಿಲ್ಲ

X ನ ಶೂನ್ಯವನ್ನು ಸಮೀಪಿಸಿದಾಗ x ನ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್‌ನ 0 ರ ಮಿತಿ ಮೈನಸ್ ಅನಂತವಾಗಿದೆ:

1 ರ ಎಲ್.ಎನ್

ಒಬ್ಬರ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಶೂನ್ಯ:

ln (1) = 0

ಅನಂತತೆಯ ಎಲ್.ಎನ್

X ಅನಂತವನ್ನು ಸಮೀಪಿಸಿದಾಗ ಅನಂತತೆಯ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್‌ನ ಮಿತಿ ಅನಂತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

ಲಿಮ್ ಹಾಗೂ ln ( ಕ್ಷ ) = ∞, ಆಗ ಕ್ಷ → ∞

ಸಂಕೀರ್ಣ ಲಾಗರಿಥಮ್

ಸಂಕೀರ್ಣ ಸಂಖ್ಯೆ z ಗಾಗಿ:

z = re ^iθ = x + iy

ಸಂಕೀರ್ಣ ಲಾಗರಿಥಮ್ ಇರುತ್ತದೆ (n = ...- 2, -1,0,1,2, ...):

ಲಾಗ್ z = ln ( r ) + i ( θ + 2nπ ) = ln ( x ( x ² + y ² )) + i · arctan ( y / x ))

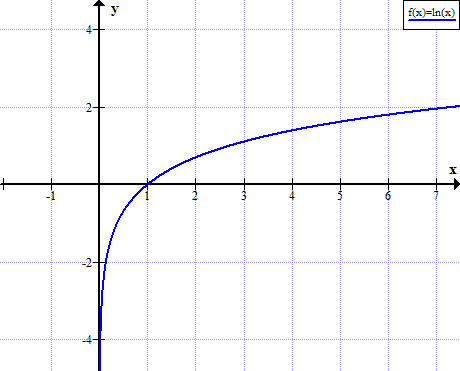
Ln (x) ನ ಗ್ರಾಫ್

x ನ ನೈಜ ಧನಾತ್ಮಕವಲ್ಲದ ಮೌಲ್ಯಗಳಿಗೆ ln (x) ಅನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ:

ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ಸ್ ಟೇಬಲ್

x	ln x
0	ಸ್ಪಷ್ಟೀಕರಿಸದ
0 +	-
0.0001	-9.210340
0.001	-6.907755
0.01	-4.605170
0.1	-2.302585
1	0
2	0.693147
ಇ ≈ 2.7183	1
3	1.098612
4	1.386294
5	1.609438
6	1.791759
7	1.945910
8	2.079442
9	2.197225
10	2.302585
20	2.995732
30	3.401197
40	3.688879
50	3.912023
60	4.094345
70	4.248495
80	4.382027
90	4.499810
100	4.605170
200	5.298317
300	5.703782
400	5.991465
500	6.214608
600	6.396930
700	6.551080
800	6.684612
900	6.802395
1000	6.907755
10000	9.210340

 

ಲಾಗರಿಥಮ್‌ನ ನಿಯಮಗಳು

 

---

ಸಹ ನೋಡಿ

• ಲಾಗರಿಥಮ್ (ಲಾಗ್)
• ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಕ್ಯಾಲ್ಕುಲೇಟರ್
• ಶೂನ್ಯದ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್
• ಒಂದರ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್
• ಇ ನ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್
• ಅನಂತತೆಯ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್
• Negative ಣಾತ್ಮಕ ಸಂಖ್ಯೆಯ ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್
• ಎಲ್ಎನ್ ವಿಲೋಮ ಕ್ರಿಯೆ
• ln (x) ಗ್ರಾಫ್
• ನೈಸರ್ಗಿಕ ಲಾಗರಿಥಮ್ ಟೇಬಲ್
• ಲಾಗರಿಥಮ್ ಕ್ಯಾಲ್ಕುಲೇಟರ್
• ಇ ಸ್ಥಿರ