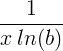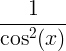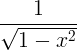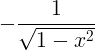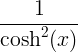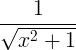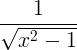Деривативни правила

Деривативни правила и закони. Деривати на табелата на функции.

• Деривативна дефиниција
• Деривативни правила
• Деривати на табелата на функции
• Изведени примери

Деривативна дефиниција

Дериват на функција е односот на разликата на вредноста на функцијата f (x) во точките x + Δx и x со Δx, кога Δx е бесконечно мал. Дериват е функција наклон или наклон на тангентната линија во точката x.

 

Втор извод

Вториот извод е даден од:

Или едноставно изведете го првиот извод:

Н-ти дериват

На n -ти дериват е пресметано со кои произлегуваат f (x) n пати.

На n -ти дериват е еднаква на Дериват на (n-1) дериват:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] "

Пример:

Пронајдете ја четвртата дериват на

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] "" "= [10 x ⁴ ]" "= [40 x ³ ]" = [120 x ² ] "= 240 x

Дериват на графикон на функција

Дериват на функција е наклон на тангенцијалната линија.

Деривативни правила

Правило за изводна сума	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Правило за деривативен производ	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Деривативно правило за количник
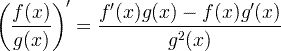Правило на дериватни ланци	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Правило за изводна сума

Кога a и b се константи.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Пример:

Пронајдете дериват на:

3 x ² + 4 x

Според правилото за збирот:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Правило за деривативен производ

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Деривативно правило за количник

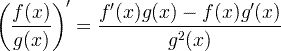
Правило на дериватни ланци

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Ова правило може подобро да се разбере со нотацијата на Лагранж:

Линеарно приближување на функцијата

За мали Δx, можеме да добиеме приближување кон f (x ₀ + Δx), кога знаеме f (x ₀ ) и f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Деривати на табелата на функции

Име на функцијата	Функција	Дериват
	f ( x )	f '( x )
Постојан	конст	0
Линеарно	x	1
Моќност	x а	секира а- 1
Експоненцијална	е x	е x
Експоненцијална	a x	a x ln a
Природен логаритам	ln ( x )
Логаритам	дневник b ( x )
Синус	грев x	cos x
Косинус	cos x	- грев x
Тангента	тен x
Аркин	arcsin x
Аркозин	лакови x
Аркантангент	arctan x
Хиперболичен синус	sinh x	cosh x
Хиперболичен косинус	cosh x	sinh x
Хиперболична тангента	танх x
Инверзен хиперболичен синус	sinh -1 x
Инверзна хиперболична косинус	cosh -1 x
Инверзна хиперболична тангента	тан -1 x

Изведени примери

Пример # 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Пример # 2

f ( x ) = грев (3 x ² )

При примена на правилото на ланецот:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Втор тест за дериват

Кога првиот извод на функција е нула во точката x ₀ .

f '( x ₀ ) = 0

Тогаш, вториот дериват во точката x ₀ , f "(x ₀ ), може да го означи типот на таа точка:

 

f "( x 0 )/ 0	локален минимум
f "( x 0 ) <0	локален максимум
f "( x 0 ) = 0	неопределени

 

---

Исто така види

• Калкулус
• Лапласова трансформација ( ℒ  )
• Калкулусни симболи