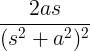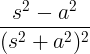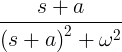Трансформација на Лаплас

Лапласовата трансформација ја претвора функцијата временски домен во функција на домен со интеграција од нула во бесконечност

на функцијата временски домен, помножена со е- ^ст .

Лапласовата трансформација се користи за брзо наоѓање решенија за диференцијални равенки и интеграли.

Изводот во временскиот домен се трансформира во множење со s во с-доменот.

Интеграцијата во временскиот домен се трансформира во поделба со s во с-доменот.

Функција за трансформација на Лаплас

Трансформацијата Лаплас е дефинирана со операторот L {}:

$F (s) = \ mathcal {L} \ лево \ {f (t) \ десно \} = \ int_ {0} ^ {\ неправилно} e ^ {- st} f (t) dt$

Инверзната трансформација на Лаплас може да се пресмета директно.

Обично инверзната трансформација е дадена од табелата за трансформации.

Име на функцијата	Функција за временски домен	Лапласова трансформација
Име на функцијата	f ( t )	F ( s ) = L { f ( t )}
Постојан	1	$\ frac {1} {s}$
Линеарно	т	$\ frac {1} {s ^ 2}$
Моќност	т ^н	$\ frac {n!} {s ^ {n + 1}}$
Моќност	т ^а	Γ ( a +1) ⋅ s ^{- ( a +1)}
Експонент	е ^на	$\ frac {1} {sa}$
Синус	грев кај	$\ frac {a} {s ^ 2 + a ^ 2}$
Косинус	кос кај	$\ frac {s} {s ^ 2 + a ^ 2}$
Хиперболичен синус	Син во	$\ frac {a} {s ^ 2-a ^ 2}$
Хиперболичен косинус	бришење на	$\ frac {s} {s ^ 2-a ^ 2}$
Растечки синус	т греши во	$\ frac {2as} {(s ^ 2 + a ^ 2) ^ 2}$
Расте косинус	t cos at	$\ frac {s ^ 2-a ^ 2} {(s ^ 2 + a ^ 2) ^ 2}$
Расипувачки синус	e ^-at sin ωt	$\ frac {\ омега} {\ лево (s + a \ десно) ^ 2 + \ омега ^ 2}$
Косинус во фаза на распаѓање	e ^-at cos ωt	$\ frac {s + a} {\ лево (s + a \ десно) ^ 2 + \ омега ^ 2}$
Делта функција	δ ( т )	1
Одложена делта	δ ( та )	е- ^како

Име на имотот	Функција за временски домен	Лапласова трансформација	Коментар
	f ( t )	F ( s )
Линеарност	af ( t ) + bg ( t )	aF ( s ) + bG ( s )	a , b се постојани
Промена на скалата	f ( кај )	$\ frac {1} {a} F \ лево (\ frac {s} {a} \ десно)$	a / 0
Смена	e ^-at f ( t )	F ( s + a )
Одложување	ѓ ( та )	e ^{- како} F ( s )
Извод	$\ frac {df (t)} {dt}$	sF ( s ) - f (0)
N-та изведба	$\ frac {d ^ nf (t)} {dt ^ n}$	s ⁿ f ( s ) - s ^{n -1}f (0) - s ^{n -2}f '(0) -...- f ^{( n -1)} (0)
Моќност	t ⁿ f ( t )	$(-1) ^ n \ frac {d ^ nF (s)} {ds ^ n}$
Интеграција	$\ int_ {0} ^ {t} f (x) dx$	$\ frac {1} {s} F (s)$
Реципрочен	$\ frac {1} {t} f (t)$	$\ int_ {s} ^ {\ неправилен} F (x) dx$
Конволуција	f ( t ) * g ( t )	F ( и ) ⋅ G ( и )	* е оператор на конволуција
Периодична функција	f ( t ) = f ( t + T )	$\ frac {1} {1-e ^ {- sT}} \ int_ {0} ^ {T} e ^ {- sx} f (x) dx$