Convolução

A convolução é a função de correlação de f (τ) com a função invertida g (t-τ).

O operador de convolução é o símbolo de asterisco * .

A convolução de f (t) e g (t) é igual à integral de f (τ) vezes f (t-τ):

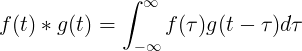
$f (t) * g (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) d \ tau$

A convolução de 2 funções discretas é definida como:

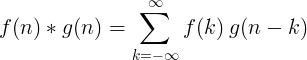
$f (n) * g (n) = \ sum_ {k = - \ infty} ^ {\ infty} f (k) \: g (nk)$

A convolução discreta bidimensional é geralmente usada para processamento de imagem.

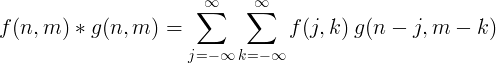
$f (n, m) * g (n, m) = \ sum_ {j = - \ infty} ^ {\ infty} \ sum_ {k = - \ infty} ^ {\ infty} f (j, k) \: g (nj, mk)$

Podemos filtrar o sinal de entrada discreto x (n) por convolução com a resposta ao impulso h (n) para obter o sinal de saída y (n).

y ( n ) = x ( n ) * h ( n )

A transformada de Fourier de uma multiplicação de 2 funções é igual à convolução das transformadas de Fourier de cada função:

ℱ { f ⋅ g } = ℱ { f } * ℱ { g }

A transformada de Fourier de uma convolução de 2 funções é igual à multiplicação das transformadas de Fourier de cada função:

ℱ { f * g } = ℱ { f } ⋅ ℱ { g }

ℱ { f ( t ) ⋅ g ( t )} = ℱ { f ( t )} * ℱ { g ( t )} = F ( ω ) * G ( ω )

ℱ { f ( t ) * g ( t )} = ℱ { f ( t )} ⋅ ℱ { g ( t )} = F ( ω ) ⋅ G ( ω )

ℱ { f ( n ) ⋅ g ( n )} = ℱ { f ( n )} * ℱ { g ( n )} = F ( k ) * G ( k )

ℱ { f ( n ) * g ( n )} = ℱ { f ( n )} ⋅ ℱ { g ( n )} = F ( k ) ⋅ G ( k )

ℒ { f ( t ) * g ( t )} = ℒ { f ( t )} ⋅ ℒ { g ( t )} = F ( s ) ⋅ G ( s )

Veja também