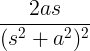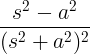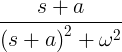Laplace Transform
- Função de transformação de Laplace
- Mesa de transformação de Laplace
- Propriedades de transformação de Laplace
- Exemplos de transformação de Laplace
A transformada de Laplace converte uma função de domínio de tempo em função de domínio s por integração de zero a infinito
da função de domínio do tempo, multiplicado por e -st .
A transformada de Laplace é usada para encontrar rapidamente soluções para equações diferenciais e integrais.
A derivação no domínio do tempo é transformada em multiplicação por s no domínio s.
A integração no domínio do tempo é transformada em divisão por s no domínio s.
Função de transformação de Laplace
A transformação de Laplace é definida com o operador L {}:
![]()
Transformada inversa de Laplace
A transformada de Laplace inversa pode ser calculada diretamente.
Normalmente, a transformação inversa é fornecida na tabela de transformações.
Mesa de transformação de Laplace
| Nome da função | Função de domínio do tempo | Transformada de Laplace |
|---|---|---|
f ( t ) |
F ( s ) = L { f ( t )} |
|
| Constante | 1 | |
| Linear | t | |
| Poder | t n |
|
| Poder | t a |
Γ ( a +1) ⋅ s - ( a +1) |
| Expoente | e em |
|
| Seno | pecado em |
|
| Cosine | porque em |
|
| Seno hiperbólico |
sinh em |
|
| Cosseno hiperbólico |
cosh em |
|
| Seno crescente |
t pecar em |
|
| Cosseno crescente |
t cos em |
|
| Seno decadente |
e -at sin ωt |
|
| Cosseno decadente |
e -at cos ωt |
|
| Função delta |
δ ( t ) |
1 |
| Delta atrasado |
δ ( ta ) |
e- como |
Propriedades de transformação de Laplace
| Nome da propriedade | Função de domínio do tempo | Transformada de Laplace | Comente |
|---|---|---|---|
f ( t ) |
F ( s ) |
||
| Linearidade | af ( t ) + bg ( t ) | aF ( s ) + bG ( s ) | a , b são constantes |
| Mudança de escala | f ( at ) |
|
a / 0 |
| Mudança | e -at f ( t ) | F ( s + a ) | |
| Demora | f ( ta ) | e - como F ( s ) | |
| Derivação |
|
sF ( s ) - f (0) | |
| N-ésima derivação |
|
s n f ( s ) - s n -1 f (0) - s n -2 f '(0) -...- f ( n -1) (0) | |
| Poder | t n f ( t ) |
|
|
| Integração |
|
|
|
| Recíproca |
|
|
|
| Convolução | f ( t ) * g ( t ) | F ( s ) ⋅ G ( s ) | * é o operador de convolução |
| Função periódica | f ( t ) = f ( t + T ) |
|
Exemplos de transformação de Laplace
Exemplo 1
Encontre a transformação de f (t):
f ( t ) = 3 t + 2 t 2
Solução:
ℒ { t } = 1 / s 2
ℒ { t 2 } = 2 / s 3
F ( s ) = ℒ { f ( t )} = ℒ {3 t + 2 t 2 } = 3ℒ { t } + 2ℒ { t 2 } = 3 / s 2 + 4 / s 3
Exemplo # 2
Encontre a transformação inversa de F (s):
F ( s ) = 3 / ( s 2 + s - 6)
Solução:
Para encontrar a transformação inversa, precisamos alterar a função do domínio s para uma forma mais simples:
F ( s ) = 3 / ( s 2 + s - 6) = 3 / [( s -2) ( s +3)] = a / ( s -2) + b / ( s +3)
[ a ( s +3) + b ( s -2)] / [( s -2) ( s +3)] = 3 / [( s -2) ( s +3)]
a ( s +3) + b ( s -2) = 3
Para encontrar a e b, obtemos 2 equações - um dos coeficientes s e o segundo do resto:
( a + b ) s + 3 a -2 b = 3
a + b = 0, 3 a -2 b = 3
a = 3/5, b = -3/5
F ( s ) = 3/5 ( s -2) - 3/5 ( s +3)
Agora F (s) podem ser transformados facilmente usando a tabela de transformações para a função expoente:
f ( t ) = (3/5) e 2 t - (3/5) e -3 t
Veja também
Advertising
CÁLCULO
- Limite
- Derivado
- Integrante
- Series
- Transformada de Laplace
- Convolução
- Símbolos de cálculo
TABELAS RÁPIDAS