Rozdelenia pravdepodobnosti
V pravdepodobnosti a štatistika distribúcia je charakteristické náhodné premenné, opisuje pravdepodobnosti náhodné premenné v každej hodnoty.
Každé rozdelenie má určitú funkciu hustoty pravdepodobnosti a funkciu rozdelenia pravdepodobnosti.
Aj keď existuje neurčitý počet rozdelení pravdepodobnosti, používa sa niekoľko bežných rozdelení.
Kumulatívna distribučná funkcia
Distribúcia pravdepodobnosti je opísaná kumulatívnou distribučnou funkciou F (x),
čo je pravdepodobnosť, že náhodná premenná X získa hodnotu menšiu alebo rovnú x:
F ( x ) = P ( X ≤ x )
Nepretržitá distribúcia
Kumulatívna distribučná funkcia F (x) sa počíta integráciou funkcie hustoty pravdepodobnosti f (u) spojitej náhodnej premennej X.
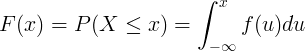
Diskrétne rozdelenie
Kumulatívna distribučná funkcia F (x) sa počíta ako súčet funkcie pravdepodobnostnej hmotnosti P (u) diskrétnej náhodnej premennej X.
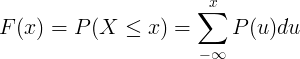
Tabuľka spojitých distribúcií
Spojitá distribúcia je distribúcia spojitej náhodnej premennej.
Príklad súvislej distribúcie
...
Tabuľka spojitých distribúcií
| Názov distribúcie | Distribučný symbol | Funkcia hustoty pravdepodobnosti (pdf) | Zlý | Rozptyl |
|---|---|---|---|---|
|
f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Normálny / gaussovský |
X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Jednotný |
X ~ U ( a , b ) |
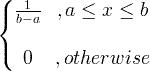 |
|
|
| Exponenciálny | X ~ exp (λ) |
|
|
|
| Gama | X ~ gama ( c , λ) |
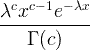 x / 0, c / 0, λ/ 0 |
|
|
| Námestie Chi |
X ~ χ 2 ( k ) |
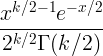 |
k |
2 k |
| Wishart | ||||
| F |
X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Prihlásiť normálne |
X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Levy | ||||
| Ryža | ||||
| Študentská t |
Tabuľka diskrétnych distribúcií
Diskrétne rozdelenie je rozdelenie diskrétnej náhodnej premennej.
Príklad diskrétneho rozdelenia
...
Tabuľka diskrétnych distribúcií
| Názov distribúcie | Distribučný symbol | Funkcia pravdepodobnosti hmotnosti (PMF) | Zlý | Rozptyl | |
|---|---|---|---|---|---|
|
f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Dvojčlen |
X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| jed |
X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Jednotný |
X ~ U ( a, b ) |
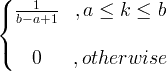 |
|
|
|
| Geometrické |
X ~ Geom ( p ) |
|
|
|
|
| Hyper-geometrické |
X ~ HG ( N , K , n ) |
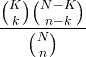 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli |
X ~ Bern ( p ) |
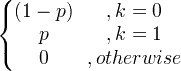 |
p |
p (1 - p ) |
|
Pozri tiež
Advertising
PRAVDEPODOBNOSŤ A ŠTATISTIKA
- Základná pravdepodobnosť
- Očakávanie
- Rozptyl
- Štandardná odchýlka
- Rozdelenia pravdepodobnosti
- Normálne rozdelenie
- Symboly štatistík
RÝCHLE TABUĽKY