Ničelna številka (0)
- Opredelitev ničelne številke
- Zgodovina ničelne številke
- Lastnosti ničelnega števila
- Kompleti, ki vsebujejo nič
Opredelitev ničelne številke
Zero je številka, ki se v matematiki uporablja za opis nobene količine ali nične količine.
Ko sta na mizi 2 jabolki in vzamemo dve jabolki, lahko rečemo, da je na mizi nič jabolk.
Ničelno število ni pozitivno in ne negativno število.
Ničelna številka je tudi nadomestna številka v drugih številkah (npr. 40,103, 170).
Ali je nič število?
Nič je število. To ni pozitivno niti negativno število.
Ničelna številka
Ničelna številka se uporablja kot nadomestni znak pri pisanju številk.
Na primer:
204 = 2 × 100 + 0 × 10 + 4 × 1
Zgodovina ničelne številke
Kdo je izumil nič številko?
Sodobni simbol 0 so izumili v Indiji v 6. stoletju, pozneje pa so ga uporabljali Perzijci in Arabci in pozneje v Evropi.
Simbol nič
Ničelno število je označeno s simbolom 0 .
Arabski številski sistem uporablja simbol ٠.
Lastnosti ničelnega števila
x predstavlja poljubno število.
| Delovanje | Pravilo | Primer |
|---|---|---|
Dodatek |
x + 0 = x |
3 + 0 = 3 |
Odštevanje |
x - 0 = x |
3 - 0 = 3 |
Množenje |
x × 0 = 0 |
5 × 0 = 0 |
Divizija |
0 ÷ x = 0 , kadar je x ≠ 0 |
0 ÷ 5 = 0 |
|
x ÷ 0 ni opredeljen |
5 ÷ 0 ni opredeljeno |
|
Povečanje |
0 x = 0 |
0 5 = 0 |
|
x 0 = 1 |
5 0 = 1 |
|
Korenina |
√ 0 = 0 |
|
Logaritem |
log b (0) ni opredeljen |
|
|
|
||
Faktor |
0! = 1 |
|
Sinus |
sin 0º = 0 |
|
Cosine |
cos 0º = 1 |
|
Tangenta |
porjavelost 0º = 0 |
|
Izvedeni finančni instrumenti |
0 '= 0 |
|
Celovito |
D 0 d x = 0 + C |
|
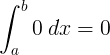 |
Nič seštevanja
Seštevanje števila in nič je enako številu:
x + 0 = x
Na primer:
5 + 0 = 5
Nič odštevanja
Odštevanje števila minus nič je enako številu:
x - 0 = x
Na primer:
5 - 0 = 5
Množenje z ničlo
Množenje števila na nič je enako nič:
x × 0 = 0
Na primer:
5 × 0 = 0
Število deljeno z ničlo
Delitev števila z ničlo ni opredeljena:
x ÷ 0 ni opredeljen
Na primer:
5 ÷ 0 ni opredeljeno
Nič deljeno s številom
Delitev ničle s številom je nič:
0 ÷ x = 0
Na primer:
0 ÷ 5 = 0
Število na ničelno moč
Moč števila, zvišanega za nič, je ena:
x 0 = 1
Na primer:
5 0 = 1
Logaritem nič
Osnovni logaritem b nič ni opredeljen:
log b (0) ni opredeljen
Ni številke, s katero bi lahko dvignili osnovo b, da bi dobili nič.
Samo neskončnost je meja osnovnega logaritma b x, ko x konvergira nič, minus neskončnost:
![]()
Kompleti, ki vsebujejo nič
Zero je element naravnih števil, celih števil, realnih števil in kompleksnih števil:
| Set | Nastavite zapis članstva |
|---|---|
| Naravna števila (nenegativna) | 0 ∈ ℕ 0 |
| Cela števila | 0 ∈ ℤ |
| Realne številke | 0 ∈ ℝ |
| Kompleksna števila | 0 ∈ ℂ |
| Racionalne številke | 0 ∈ ℚ |
Je nič sodo ali liho število?
Nabor parnih števil je:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Nabor lihih števil je:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Zero je celo število, večkratnik 2:
0 × 2 = 0
Zero je član nabora parnih števil:
0 ∈ {2 k , k ∈ℤ}
Torej nič je sodo število in ne liho število.
Ali je nič naravno število?
Za nabor naravnih števil obstajata dve definiciji.
Nabor nenegativnih celih števil:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Nabor pozitivnih celih števil:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Zero je član niza nenegativnih celih števil:
0 ∈ ℕ 0
Zero ni član nabora pozitivnih celih števil:
0 ∉ ℕ 1
Ali je nič celo število?
Obstajajo tri definicije za celotna števila:
Nabor celoštevilskih števil:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Nabor nenegativnih celih števil:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
Nabor pozitivnih celih števil:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Zero je član niza celoštevilskih števil in niza celo negativnih celih števil:
0 ∈ ℤ
0 ∈ ℕ 0
Zero ni član nabora pozitivnih celih števil:
0 ∉ ℕ 1
Ali je nič celo število?
Nabor celoštevilskih števil:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Zero je član nabora celoštevilskih števil:
0 ∈ ℤ
Torej nič je celo število.
Je nič racionalno število?
Racionalno število je število, ki ga lahko izrazimo kot količnik dveh celih števil:
ℚ = { n / m ; n , m ∈ℤ}
Zero lahko zapišemo kot količnik dveh celih števil.
Na primer:
0 = 0/3
Torej nič je racionalno število.
Ali je nič pozitivno število?
Pozitivno število je opredeljeno kot število, ki je večje od nič:
x / 0
Na primer:
5/ 0
Ker nič ni večja od nič, ni pozitivno število.
Ali je nič osnovno število?
Število 0 ni praštevilo.
Nič ni pozitivno število in ima neskončno število deliteljev.
Najnižje praštevilo je 2.