e tairiseach

tairiseach matamaiticiúil í e tairiseach nó uimhir Euler . Tá an r-tairiseach fíor agus uimhir neamhréasúnach.

e = 2.718281828459 ...

Sainmhíniú ar e
Airíonna e
Bonn e logarithm
Feidhm easpónantúil
Foirmle Euler

Sainmhíniú ar e

Sainmhínítear an tairiseach e mar an teorainn:

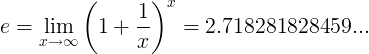
$e = \ lim_ {x \ rightarrow \ infty} \ ar chlé (1+ \ frac {1} {x} \ deas) ^ x = 2.718281828459 ...$

Sainmhínithe malartacha

Sainmhínítear an tairiseach e mar an teorainn:

$e = \ lim_ {x \ rightarrow 0} \ ar chlé (1+ \ deas x) ^ \ frac {1} {x}$

Sainmhínítear an tairiseach e mar an tsraith gan teorainn:

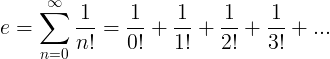
$e = \ sum_ {n = 0} ^ {\ infty} \ frac {1} {n!} = \ frac {1} {0!} + \ frac {1} {1!} + \ frac {1} { 2!} + \ Frac {1} {3!} + ...$

Airíonna e

Cómhalartach e

Is é cómhalartach e an teorainn:

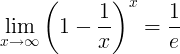
$\ lim_ {x \ rightarrow \ infty} \ ar chlé (1- \ frac {1} {x} \ deas) ^ x = \ frac {1} {e}$

Díorthaigh e

Is é díorthach na feidhme easpónantúla an fheidhm easpónantúil:

( e ^x ) '= e ^x

Is é díorthach na feidhme logarithm nádúrtha an fheidhm chómhalartach:

(log _e x ) '= (ln x )' = 1 / x

Comhtháthaithe e

Is í an eilimint éiginnte den fheidhm easpónantúil e ^x an fheidhm easpónantúil e ^x .

∫ e ^x dx = e ^x + c

Is é an chuid éiginnte éiginnte den fheidhm logarithm nádúrtha log _e x :

∫ log _e x dx = ∫ ln x dx = x ln x - x + c

Is í an eilimint chinnte ó 1 go e den fheidhm chómhalartach 1 / x ná 1:

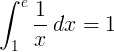
$\ int_ {1} ^ {e} \ frac {1} {x} \: dx = 1$

Bonn e logarithm

Sainmhínítear logarithm nádúrtha uimhir x mar bhun-logarithm x:

ln x = log _e x

Feidhm easpónantúil

Sainmhínítear an fheidhm easpónantúil mar seo a leanas:

f ( x ) = exp ( x ) = e ^x

Foirmle Euler

Tá an uimhir ^aitheantais ag an uimhir chasta e ^iθ :

e ^iθ = cos ( θ ) + i sin ( θ )

Is mise an t-aonad samhailteach (fréamh chearnach -1).

Is é θ aon fhíoruimhir.