Uimhir nialais (0)
- Sainmhíniú ar uimhir nialais
- Stair uimhreacha nialais
- Airíonna nialas uimhreacha
- Tacair ina bhfuil nialas
Sainmhíniú ar uimhir nialais
Is uimhir í nialas a úsáidtear sa mhatamaitic chun cur síos a dhéanamh ar chainníocht nó ar chainníocht null.
Nuair a bhíonn 2 úll ar an mbord agus muid ag glacadh an 2 úll, is féidir linn a rá go bhfuil úlla nialasacha ar an mbord.
Ní uimhir dhearfach í an uimhir nialasach agus ní uimhir dhiúltach í.
Is dhigit áitritheora é an nialas freisin i líon eile (m.sh .: 40,103, 170).
An bhfuil nialas mar uimhir?
Is uimhir í nialas. Ní uimhir dearfach ná diúltach í.
Uimhir dhigit
Úsáidtear an dhigit nialasach mar áititheoir agus uimhreacha á scríobh.
Mar shampla:
204 = 2 × 100 + 0 × 10 + 4 × 1
Stair uimhreacha nialais
Cé a chum an uimhir nialasach?
Ceapadh an tsiombail 0 nua-aimseartha san India sa 6ú haois, a d'úsáid na Peirsigh agus na hArabaigh níos déanaí agus níos déanaí san Eoraip.
Siombail nialas
Cuirtear an uimhir nialas in iúl leis an tsiombail 0 .
Úsáideann an córas uimhriúil Araibis an tsiombail ٠.
Airíonna nialas uimhreacha
Léiríonn x uimhir ar bith.
| Oibríocht | Riail | Sampla |
|---|---|---|
Suimiú |
x + 0 = x |
3 + 0 = 3 |
Dealú |
x - 0 = x |
3 - 0 = 3 |
Iolrú |
x × 0 = 0 |
5 × 0 = 0 |
Rannán |
0 ÷ x = 0 , nuair a bhíonn x ≠ 0 |
0 ÷ 5 = 0 |
|
tá x ÷ 0 neamhshainithe |
Tá 5 ÷ 0 neamhshainithe |
|
Exponentiation |
0 x = 0 |
0 5 = 0 |
|
x 0 = 1 |
5 0 = 1 |
|
Fréamh |
√ 0 = 0 |
|
Logarithm |
tá log b (0) neamhshainithe |
|
|
|
||
Fachtóir |
0! = 1 |
|
Sín |
sin 0º = 0 |
|
Cosine |
cos 0º = 1 |
|
Tadhlaí |
tan 0º = 0 |
|
Díorthach |
0 '= 0 |
|
Lárnach |
∫ 0 d x = 0 + C. |
|
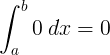 |
Suim nialais
Is ionann uimhir agus nialas a chur leis an uimhir:
x + 0 = x
Mar shampla:
5 + 0 = 5
Dealú nialais
Tá dealú uimhir lúide nialas cothrom leis an uimhir:
x - 0 = x
Mar shampla:
5 - 0 = 5
Iolrú faoi nialas
Tá iolrú líon uaireanta nialas cothrom le nialas:
x × 0 = 0
Mar shampla:
5 × 0 = 0
Líon roinnte ar nialas
Ní shainmhínítear uimhir a roinnt ar nialas:
tá x ÷ 0 neamhshainithe
Mar shampla:
Tá 5 ÷ 0 neamhshainithe
Nialais roinnte ar uimhir
Is nialas an uimhir a roinnt ar nialas:
0 ÷ x = 0
Mar shampla:
0 ÷ 5 = 0
Líon go dtí an chumhacht nialasach
Is é cumhacht uimhir a ardaíonn nialas:
x 0 = 1
Mar shampla:
5 0 = 1
Logarithm nialas
Tá bun logarithm nialas neamhshainithe:
tá log b (0) neamhshainithe
Níl aon uimhir ar féidir linn an bonn b a ardú leis chun nialas a fháil.
Níl ach teorainn an logarithm bonn b de x, nuair a thagann x le chéile nialas, lúide an Infinity:
![]()
Tacair ina bhfuil nialas
Is eilimint í eilimint de na huimhreacha nádúrtha, slánuimhreacha, fíoruimhreacha agus tacair uimhreacha casta:
| Socraigh | Socraigh nodaireacht ballraíochta |
|---|---|
| Uimhreacha nádúrtha (neamh-dhiúltach) | 0 ∈ ℕ 0 |
| Uimhreacha slánuimhir | 0 ∈ ℤ |
| Fíoruimhreacha | 0 ∈ ℝ |
| Uimhreacha casta | 0 ∈ ℂ |
| Uimhreacha réasúnach | 0 ∈ ℚ |
An bhfuil uimhir chothrom nialasach nó corr?
Is é tacar na n-uimhreacha cothrom:
{..., -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ...}
Is é an tacar corr-uimhreacha:
{..., -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, ...}
Is iolra slánuimhir 2 é nialas:
0 × 2 = 0
Tá nialas ina bhall de na huimhreacha cothroma a leagtar síos:
0 ∈ {2 k , k ∈ℤ}
Mar sin is uimhir chothrom í nialas agus ní corr-uimhir.
An uimhir nádúrtha í nialas?
Tá dhá shainmhíniú ann maidir leis na huimhreacha nádúrtha atá leagtha síos.
An tsraith slánuimhreacha neamh-dhiúltacha:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
An tsraith slánuimhreacha dearfacha:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Tá nialas ina bhall den tsraith slánuimhreacha neamh-dhiúltacha:
0 ∈ ℕ 0
Níl Zero ina bhall den tsraith slánuimhreacha dearfacha:
0 ∉ ℕ 1
An slánuimhir é nialas?
Tá trí shainmhíniú ann do na slánuimhreacha:
An tacar uimhreacha slánuimhir:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
An tsraith slánuimhreacha neamh-dhiúltacha:
ℕ 0 = {0,1,2,3,4,5,6,7,8, ...}
An tsraith slánuimhreacha dearfacha:
ℕ 1 = {1,2,3,4,5,6,7,8, ...}
Tá nialas ina bhall den tsraith uimhreacha slánuimhir agus den tsraith slánuimhreacha neamh-dhiúltacha:
0 ∈ ℤ
0 ∈ ℕ 0
Níl Zero ina bhall den tsraith slánuimhreacha dearfacha:
0 ∉ ℕ 1
An slánuimhir í nialas?
An tacar uimhreacha slánuimhir:
ℤ = {0,1,2,3,4,5,6,7,8, ...}
Tá nialas ina bhall den tsraith uimhreacha slánuimhir:
0 ∈ ℤ
Mar sin is uimhir slánuimhir í nialas.
An uimhir réasúnach í nialas?
Is í uimhir réasúnach uimhir is féidir a chur in iúl mar chomhrann dhá uimhir slánuimhir:
ℚ = { n / m ; n , m ∈ℤ}
Is féidir nialas a scríobh mar chomhrann de dhá uimhir slánuimhir.
Mar shampla:
0 = 0/3
Mar sin is uimhir réasúnach í nialas.
An uimhir dhearfach í nialas?
Sainmhínítear uimhir dhearfach mar uimhir is mó ná nialas:
x / 0
Mar shampla:
5/ 0
Ós rud é nach mó ná nialas nialas, ní uimhir dhearfach í.
An uimhir phríomha í nialas?
Ní uimhir phríomha í an uimhir 0.
Ní uimhir dhearfach í nialas agus tá líon gan teorainn roinnteoirí ann.
Is é 2 an uimhir phríomha is ísle.