Diffríochtaí

Maidir le dóchúlacht agus staitisticí, is é athraitheas athróg randamach meánluach an achair chearnaigh ón meánluach. Léiríonn sé an chaoi a ndéantar an athróg randamach a dháileadh gar don mheánluach. Tugann athraitheas beag le fios go ndéantar an athróg randamach a dháileadh gar don mheánluach. Tugann athraitheas mór le fios go ndéantar an athróg randamach a dháileadh i bhfad ón meánluach. Mar shampla, le dáileadh gnáth, beidh athraitheas beag ag cuar caol an chloig agus beidh athraitheas mór i gcuar cloig leathan.

Sainmhíniú ar athraitheas

Is é athraitheas athróg randamach X luach ionchasach na gcearnóg difríochta X agus an luach ionchais μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

Ón sainmhíniú ar an athraitheas is féidir linn a fháil

σ ² = Var ( X ) = E ( X ² ) - μ ²

Athróg randamach leanúnach a athrú

Maidir le hathróg randamach leanúnach le meánluach μ agus feidhm dlús dóchúlachta f (x):

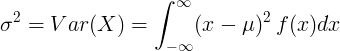
$\ sigma ^ 2 = Var (X) = \ int _ {- \ infty} ^ {\ infty} (x- \ mu) ^ 2 \: f (x) dx$

nó

$Var (X) = \ ar chlé [\ int _ {- \ infty} ^ {\ infty} x ^ 2 \: f (x) dx \ right] - \ mu ^ 2$

Athróg randamach scoite a athrú

Maidir le hathróg randamach scoite X le meánluach μ agus maisfheidhm dóchúlachta P (x):

$\ sigma ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

nó

$Var (X) = \ ar chlé [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ deas] - \ mu ^ 2$

Airíonna athraitheas

Nuair is athróga randamacha neamhspleácha iad X agus Y:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Diall caighdeánach ►

Diffríochtaí

Sainmhíniú ar athraitheas

Athróg randamach leanúnach a athrú

Athróg randamach scoite a athrú

Airíonna athraitheas

Var ( X + Y ) = Var ( X ) + Var ( Y )

Féach freisin

PROBABILITY & STAITISTICÍ

TÁBLAÍ RAPID