Dáileadh Dóchúlachta
Maidir le dóchúlacht agus staitisticí is tréith athróg randamach é dáileadh , déanann sé cur síos ar dhóchúlacht an athróg randamach i ngach luach.
Tá feidhm dlús dóchúlachta áirithe agus feidhm dáilte dóchúlachta ag gach dáileadh.
Cé go bhfuil líon éiginnte dáiltí dóchúlachta ann, tá roinnt dáiltí coitianta in úsáid.
Feidhm dáilte carnach
Déantar cur síos ar dháileadh na dóchúlachta leis an bhfeidhm dáileacháin charnach F (x),
is é sin an dóchúlacht go bhfaighidh athróg randamach X luach níos lú ná nó cothrom le x:
F ( x ) = P ( X ≤ x )
Dáileadh leanúnach
Ríomhtar an fheidhm dáileacháin charnach F (x) trí chomhtháthú na feidhme dlúis dóchúlachta f (u) d'athróg randamach leanúnach X.
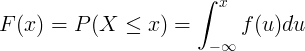
Dáileadh scoite
Ríomhtar an fheidhm dáileacháin charnach F (x) trí shuimiú na feidhme maise dóchúlachta P (u) d'athróg randamach scoite X.
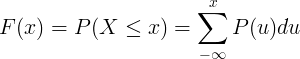
Tábla dáiltí leanúnacha
Is éard is dáileadh leanúnach ann dáileadh athróg randamach leanúnach.
Sampla dáileacháin leanúnach
...
Tábla dáiltí leanúnacha
| Ainm dáilte | Siombail dáilte | Feidhm dlús dóchúlachta (pdf) | Meán | Diffríochtaí |
|---|---|---|---|---|
|
f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Gnáth / gaussach |
X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Éide |
X ~ U ( a , b ) |
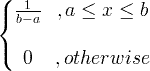 |
|
|
| Easpónantúil | X ~ exp (λ) |
|
|
|
| Gáma | X ~ gáma ( c , λ) |
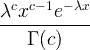 x / 0, c / 0, λ/ 0 |
|
|
| Chi cearnach |
X ~ χ 2 ( k ) |
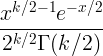 |
k |
2 k |
| Wishart | ||||
| F |
X ~ F ( k 1 , k 2 ) |
|||
| Béite | ||||
| Weibull | ||||
| Log-gnáth |
X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Tobhach | ||||
| Rís | ||||
| Mac léinn t |
Tábla dáiltí scoite
Is éard atá i ndáileadh scoite ná dáileadh athróg randamach scoite.
Sampla dáilte scoite
...
Tábla dáiltí scoite
| Ainm dáilte | Siombail dáilte | Feidhm mais dóchúlachta (pmf) | Meán | Diffríochtaí | |
|---|---|---|---|---|---|
|
f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Binomial |
X ~ Bin ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson |
X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Éide |
X ~ U ( a, b ) |
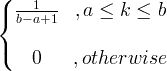 |
|
|
|
| Geoiméadrach |
X ~ Geom ( p ) |
|
|
|
|
| Hyper-geoiméadrach |
X ~ HG ( N , K , n ) |
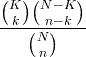 |
N = 0,1,2, ... K = 0,1, .., N. n = 0,1, ..., N. |
|
|
| Bernoulli |
X ~ Bern ( p ) |
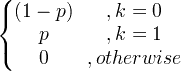 |
p |
p (1- p ) |
|
Féach freisin
Advertising
PROBABILITY & STAITISTICÍ
- Dóchúlacht bunúsach
- Ionchas
- Diffríochtaí
- Diall caighdeánach
- Dáileadh dóchúlachta
- Dáileadh gnáth
- Siombailí staitisticí
TÁBLAÍ RAPID