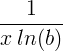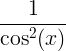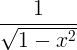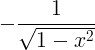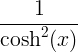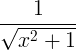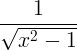Mga panuntunang nagmula

Mga patakaran at batas na nagmula sa hango. Derivatives ng talahanayan ng pag-andar.

• Kahulugan na hango
• Mga panuntunang nagmula
• Derivatives ng talahanayan ng pag-andar
• Mga halimbawa na nagmula

Kahulugan na hango

Ang hango ng isang pagpapaandar ay ang ratio ng pagkakaiba ng halaga ng pag-andar f (x) sa mga puntong x + Δx at x na may Δx, kapag ang Δx ay maliit na infinitesimally. Ang derivative ay ang function slope o slope ng tangent line sa point x.

 

Pangalawang hango

Ang pangalawang derivative ay ibinibigay ng:

O kunin lamang ang unang hango:

Nth derivative

Ang n derivative ay kinakalkula sa pamamagitan ng pagmula ng f (x) n beses.

Ang n derivative ay katumbas ng derivative ng (n-1) derivative:

f ^{( n )} ( x ) = [ f ^{( n -1)} ( x )] '

Halimbawa:

Hanapin ang ika-apat na hango ng

f ( x ) = 2 x ⁵

f ⁽⁴⁾ ( x ) = [2 x ⁵ ] "" "= [10 x ⁴ ]" "= [40 x ³ ]" = [120 x ² ] '= 240 x

Hango sa grapiko ng pagpapaandar

Ang hango ng isang pag-andar ay ang slop ng tangential line.

Mga panuntunang nagmula

Panuntunan sa kabuuan ng hango	( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )
Panuntunan ng produkto na nagmula	( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )
Panuntunang nagmula sa hango
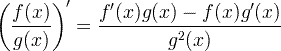Panuntunan sa derivative chain	f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Panuntunan sa kabuuan ng hango

Kapag ang a at b ay pare-pareho.

( af ( x ) + bg ( x )) '= af' ( x ) + bg ' ( x )

Halimbawa:

Hanapin ang hinalang ng:

3 x ² + 4 x.

Ayon sa panuntunan sa kabuuan:

a = 3, b = 4

f ( x ) = x ² , g ( x ) = x

f ' ( x ) = 2 x , g' ( x ) = 1

(3 x ² + 4 x ) '= 3⋅2 x + 4⋅1 = 6 x + 4

Panuntunan ng produkto na nagmula

( f ( x ) ∙ g ( x )) '= f' ( x ) g ( x ) + f ( x ) g ' ( x )

Panuntunang nagmula sa hango

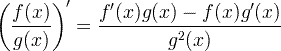
Panuntunan sa derivative chain

f ( g ( x )) '= f' ( g ( x )) ∙ g ' ( x )

Ang panuntunang ito ay maaaring mas maintindihan sa notasyon ni Lagrange:

Pag-andar sa linear na pag-andar

Para sa maliit na Δx, makakakuha tayo ng isang approximation sa f (x ₀ + Δx), kapag alam natin f (x ₀ ) at f '(x ₀ ):

f ( x ₀ + Δ x ) ≈ f ( x ₀ ) + f '( x ₀ ) ⋅Δ x

Derivatives ng talahanayan ng pag-andar

Pangalan ng pagpapaandar	Pag-andar	Hango
	f ( x )	f '( x )
Patuloy	Const	0
Linear	x	1
Lakas	x a	palakol a- 1
Exponential	e x	e x
Exponential	isang x	isang x ln a
Likas na logarithm	ln ( x )
Logarithm	mag-log b ( x )
Sine	kasalanan x	cos x
Cosine	cos x	-kakasalanan x
Tangent	tan x
Arcsine	arcsin x
Arccosine	mga arko x
Arctangent	arctan x
Hyperbolic sine	sinh x	cosh x
Hyperbolic cosine	cosh x	sinh x
Hyperbolic tangent	tanh x
Kabaligtaran na hyperbolic sine	sinh -1 x
Kabaligtaran hyperbolic cosine	cosh -1 x
Kabaligtaran na hyperbolic tangent	tanh -1 x

Mga halimbawa na nagmula

Halimbawa # 1

f ( x ) = x ³ +5 x ² + x +8

f ' ( x ) = 3 x ² + 2⋅5 x + 1 + 0 = 3 x ² +10 x +1

Halimbawa # 2

f ( x ) = kasalanan (3 x ² )

Kapag inilalapat ang panuntunan sa kadena:

f ' ( x ) = cos (3 x ² ) ⋅ [3 x ² ]' = cos (3 x ² ) ⋅ 6 x

Pangalawang derivative test

Kapag ang unang hango ng isang pagpapaandar ay zero sa puntong x ₀ .

f '( x ₀ ) = 0

Pagkatapos ang pangalawang hango sa puntong x ₀ , f "(x ₀ ), ay maaaring ipahiwatig ang uri ng puntong iyon:

 

f "( x 0 )/ 0	lokal na minimum
f "( x 0 ) <0	lokal na maximum
f "( x 0 ) = 0	hindi natukoy

 

---

Tingnan din

• Calculus
• Laplace transform ( ℒ  )
• Mga simbolo ng Calculus