Arcsine virka
bogadráttur (x), sin -1 (x), andhverfur sinus virka.
Arcsin skilgreining
Arkarsínusi X er skilgreint eins andhverfs sine fall af X þegar lyf -1≤x≤1.
Þegar sinus y er jafn x:
sin y = x
Þá er bogasínan af x jöfn andhverfu sinusaðgerðinni x, sem er jöfn y:
bogalaga x = sin -1 x = y
Dæmi
boga 1 = sin -1 1 = π / 2 rad = 90 °
Graf af boga
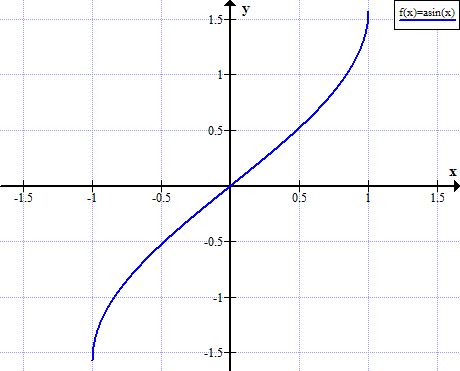
Arcsin ræður
| Regluheiti | Regla |
|---|---|
| Sine of archesine | sin (boga x ) = x |
| Bogbogasínus | bogadráttur (sin x ) = x +2 k π, þegar k ∈ℤ ( k er heiltala) |
| Arcsin af neikvæðum rökum | bogbogi (- x ) = - bogbogi x |
| Viðbótarhorn | bogadráttur x = π / 2 - arccos x = 90 ° - arccos x |
| Arcsin summan | boga α + boga ( β ) = boga ( α√ (1- β 2 ) + β√ (1- α 2 ) ) |
| Arcsin munur | arcsin α - arcsin ( β ) = arcsin ( α√ (1- β 2 ) - β√ (1- α 2 ) ) |
| Kósínus bogbogans | |
| Tangent af bogasíni | |
| Afleiða boga | 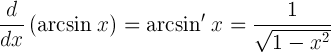 |
| Óákveðinn óaðskiljanlegur boga |
Arcsin borð
| x | bogadráttur (x) (rad) |
bogadráttur (x) (°) |
|---|---|---|
| -1 | -π / 2 | -90 ° |
| -√ 3 /2 | -π / 3 | -60 ° |
| -√ 2 /2 | -π / 4 | -45 ° |
| -1/2 | -π / 6 | -30 ° |
| 0 | 0 | 0 ° |
| 1/2 | π / 6 | 30 ° |
| √ 2 /2 | π / 4 | 45 ° |
| √ 3 /2 | π / 3 | 60 ° |
| 1 | π / 2 | 90 ° |
Sjá einnig
- Sinus virkni
- Arccosine virka
- Arctan virka
- Arcsin reiknivél
- Gráður í radíana breytir
- Arcsin af 0
- Arcsin af 1
- Arcsin óendanleikans
- Arcsin línurit
- Arcsin afleiða
- Arcsin óaðskiljanlegur
- Synd boga
- Cos af boga
- Brún af boganum
Advertising