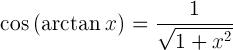Función arcangente
Arctan (x), tan -1 (x), función de tangente inversa .
Definición arctan
La arcotangente de x se define como la función tangente inversa de x cuando x es real (x ∈ℝ ).
Cuando la tangente de y es igual ax:
tan y = x
Entonces la arcotangente de x es igual a la función tangente inversa de x, que es igual ay:
arctan x = tan -1 x = y
Ejemplo
arctan 1 = tan -1 1 = π / 4 rad = 45 °
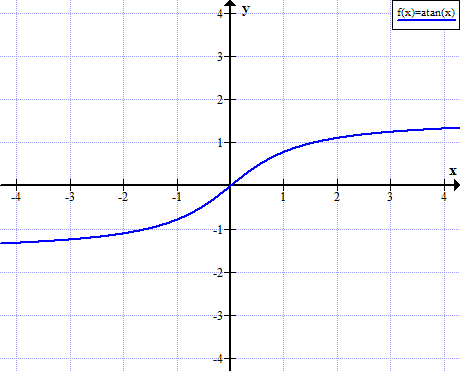
Gráfico de arctan
Reglas de Arctan
| Nombre de la regla | Regla |
|---|---|
| Tangente de arcangente |
tan (arctan x ) = x |
| Arctan de argumento negativo |
arctan (- x ) = - arctan x |
| Suma de Arctan |
arctan α + arctan β = arctan [( α + β ) / (1- αβ )] |
| Diferencia de Arctan |
arctan α - arctan β = arctan [( α - β ) / (1+ αβ )] |
| Seno de arcangente |
|
| Coseno de arcangente |
|
| Argumento recíproco |
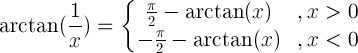 |
| Arctan de arcsin |
|
| Derivado de arctan |
|
| Integral indefinida de arctan |
|
Mesa Arctan
| x | arctan (x) (rad) |
arctan (x) (°) |
|---|---|---|
| -∞ | -π / 2 | -90 ° |
| -3 | -1,2490 | -71.565 ° |
| -2 | -1.1071 | -63.435 ° |
| -√ 3 | -π / 3 | -60 ° |
| -1 | -π / 4 | -45 ° |
| -1 / √ 3 | -π / 6 | -30 ° |
| -0,5 | -0,4636 | -26,565 ° |
| 0 | 0 | 0 ° |
| 0,5 | 0.4636 | 26.565 ° |
| 1 / √ 3 | π / 6 | 30 ° |
| 1 | π / 4 | 45 ° |
| √ 3 | π / 3 | 60 ° |
| 2 | 1.1071 | 63.435 ° |
| 3 | 1,2490 | 71.565 ° |
| ∞ | π / 2 | 90 ° |
Ver también
- Función tangente
- Función arcoseno
- Función arcoseno
- Arctan de 0
- Arctan de 1
- Arctan de 2
- Arctan del infinito
- Derivado de arctan
- Integral de arctan
- Seno de arctan
- Coseno de arctano
- Gráfico de Arctan
- Calculadora Arctan
- Conversor de grados a radianes
Advertising
TRIGONOMETRÍA
MESAS RÁPIDAS