Правила на логаритам

На база б логаритам на бројот е експонент дека ние треба да се подигне на база со цел да се добие број.

Дефиниција на логаритам

Кога b се подигне на моќноста на y е еднакво x:

b y = x

Тогаш, основниот б логаритам на x е еднаков на y:

дневник b ( x ) = y

На пример кога:

2 4 = 16

Потоа

дневник 2 (16) = 4

Логаритам како инверзна функција на експоненцијална функција

Логаритамската функција,

y = дневник b ( x )

е инверзна функција на експоненцијалната функција,

x = b y

Значи, ако ја пресметаме експоненцијалната функција на логаритмот на x (x/ 0),

f ( f -1 ( x )) = b лог b ( x ) = x

Или ако го пресметаме логаритмот на експоненцијалната функција на x,

f -1 ( f ( x )) = дневник b ( b x ) = x

Природен логаритам (ln)

Природен логаритам е логаритам на основата д:

ln ( x ) = дневник e ( x )

Кога е константа е бројот:

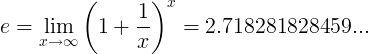
e = \ lim_ {x \ rightarrow \ infty} \ лево (1+ \ frac {1} {x} \ десно) ^ x = 2.718281828459 ...

или

e = \ lim_ {x \ rightarrow 0} \ лево (1+ \ десно x) ^ \ frac {1} {x}

 

Погледнете: Природен логаритам

Инверзна пресметка на логаритмот

Инверзниот логаритам (или антилогаритмот) се пресметува со подигнување на основата b до логаритмот y:

x = дневник -1 ( y ) = b y

Логаритамска функција

Логаритамската функција ја има основната форма на:

f ( x ) = дневник b ( x )

Правила на логаритам

Име на правило Правило
Правило на производот логаритам
 дневник b ( x ∙ y ) = дневник b ( x ) + дневник b ( y )
Правило за количник на логаритам
 дневник b ( x / y ) = дневник b ( x ) - дневник b ( y )
Правило за моќност на логаритмот
 дневник b ( x y ) = y ∙ дневник b ( x )
Правило за прекинувач на основата на логаритмот
 дневник b ( c ) = 1 / log c ( b )
Правило за промена на основата на логаритмот
 дневник b ( x ) = дневник c ( x ) / дневник c ( b )
Дериват на логаритам
 f ( x ) = дневник b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
Интеграл на логаритмот
 ∫ дневник b ( x ) dx = x ∙ (најава b ( x ) - 1 / ln ( b ) ) + C
Логаритам на негативен број
 дневникот b ( x ) е недефиниран кога x ≤ 0
Логаритам од 0
 дневникот б (0) е недефиниран
\ lim_ {x \ до 0 ^ +} \ textup {log} _b (x) = - \ неправилно
Логаритам од 1
 дневник b (1) = 0
Логаритам на основата
 дневник b ( b ) = 1
Логаритам на бесконечност
 lim log b ( x ) = ∞, кога x → ∞

Погледнете: Правила на логаритам

 

Правило на производот логаритам

Логаритмот на множењето на x и y е збир на логаритам на x и логаритам на y.

дневник b ( x ∙ y ) = дневник b ( x ) + дневник b ( y )

На пример:

дневник 10 (3 ∙ 7) = дневник 10 (3) + дневник 10 (7)

Правило за количник на логаритам

Логаритмот на поделбата на x и y е разликата на логаритмот на x и логаритмот на y.

дневник b ( x / y ) = дневник b ( x ) - дневник b ( y )

На пример:

најавува 10 (3 / 7) = најавува 10 (3) - се најавите 10 (7)

Правило за моќност на логаритмот

Логаритмот на x подигнат на моќта на y е y повеќе од логаритмот на x.

дневник b ( x y ) = y ∙ дневник b ( x )

На пример:

лог 10 (2 8 ) = 8 ∙ лог 10 (2)

Правило за прекинувач на основата на логаритмот

Логаритмот на основата b на c е 1 поделен со логаритамот на основата c на b.

дневник b ( c ) = 1 / log c ( b )

На пример:

дневник 2 (8) = 1 / дневник 8 (2)

Правило за промена на основата на логаритмот

Основниот б логаритам на x е логаритам на основата c на x поделен со логаритмот на основата c на b.

дневник b ( x ) = дневник c ( x ) / дневник c ( b )

На пример, за да го пресметаме дневникот 2 (8) во калкулаторот, треба да ја смениме основата на 10:

дневник 2 (8) = дневник 10 (8) / дневник 10 (2)

Погледнете: правило за промена на основата на дневникот

Логаритам на негативен број

Основата б реален логаритам на x кога x <= 0 е недефинирана кога x е негативна или еднаква на нула:

дневникот b ( x ) е недефиниран кога x ≤ 0

Погледнете: дневник на негативен број

Логаритам од 0

Логаритмот на нулта основа b не е дефиниран:

дневникот б (0) е недефиниран

Границата на логаритамот на основата b на x, кога x се приближува до нула, е минус бесконечност:

\ lim_ {x \ до 0 ^ +} \ textup {log} _b (x) = - \ неправилно

Погледнете: дневник на нула

Логаритам од 1

Основниот б логаритам е нула:

дневник b (1) = 0

На пример, два логаритма на основата на два е нула:

дневник 2 (1) = 0

Погледнете: дневник на еден

Логаритам на бесконечност

Границата на логаритамот на основата b на x, кога x се приближува до бесконечноста, е еднаква на бесконечноста:

lim log b ( x ) = ∞, кога x → ∞

Погледнете: дневник на бесконечност

Логаритам на основата

Основниот б логаритам на б е еден:

дневник b ( b ) = 1

На пример, логаритмот на основата два е два:

дневник 2 (2) = 1

Дериват на логаритам

Кога

f ( x ) = дневник b ( x )

Потоа, дериватот на f (x):

f ' ( x ) = 1 / ( x ln ( b ))

Погледнете: дериват на дневник

Интеграл на логаритмот

Интеграл на логаритмот на x:

∫ дневник b ( x ) dx = x ∙ (најава b ( x ) - 1 / ln ( b ) ) + C

На пример:

∫ дневник 2 ( x ) dx = x ∙ (најава 2 ( x ) - 1 / ln (2) ) + C

Приближување на логаритмот

лог 2 ( x ) ≈ n + ( x / 2 n - 1),

Комплексен логаритам

За комплексен број z:

z = повторно iθ = x + iy

Комплексот логаритам ќе биде (n = ...- 2, -1,0,1,2, ...):

Пријавете z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · арктан ( y / x ))

Проблеми и одговори на логаритам

Проблем # 1

Пронајдете x за

лог 2 ( x ) + лог 2 ( x -3) = 2

Решение:

Користење на правилото за производот:

дневник 2 ( x ∙ ( x -3)) = 2

Промена на формата на логаритам според дефиницијата на логаритам:

x ∙ ( x -3) = 2 2

Или

x 2 -3 x -4 = 0

Решавање на квадратната равенка:

x 1,2 = [3 √ √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

Бидејќи логаритмот не е дефиниран за негативни броеви, одговорот е:

x = 4

Проблем # 2

Пронајдете x за

лог 3 ( x +2) - лог 3 ( x ) = 2

Решение:

Користење на правилото за количник:

лог 3 (( x +2) / x ) = 2

Промена на формата на логаритам според дефиницијата на логаритам:

( x +2) / x = 3 2

Или

x +2 = 9 x

Или

8 x = 2

Или

x = 0,25

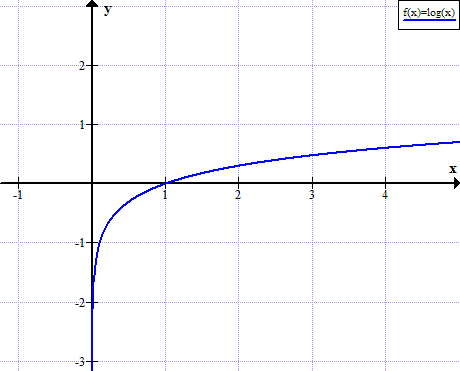
График на дневник (x)

лог (x) не е дефиниран за реални не позитивни вредности на x:

Табела за логаритми

x дневник 10 x дневник 2 x дневник е x
0 недефинирано недефинирано недефинирано
0 + - - -
0.0001 -4 -13.287712 -9.210340
0,001 -3 -9.965784 -6.907755
0,01 -2 -6.643856 -4.605170
0,1 -1 -3.321928 година -2.302585
1 0 0 0
2 0,301030 1 0.693147
3 0,477121 1.584963 1.098612
4 0,602060 2 1.386294
5 0,698970 2.321928 година 1.609438
6 0,778151 2.584963 1.791759
7 0,845098 2.807355 1.945910
8 0,903090 3 2.079442
9 0,954243 3.169925 2.197225 година
10 1 3.321928 година 2.302585
20 1.301030 4.321928 година 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 година 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 година 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

Калкулатор за логаритам

 

Исто така види

Advertising

АЛГЕБРА
БРЗИ ТАБЕЛИ