Варијанса

Во веројатност и статистика, варијансата на случајна променлива е просечната вредност на квадратното растојание од средната вредност. Тоа претставува начинот на распределување на случајната променлива близу до средната вредност. Мала варијанса покажува дека случајната променлива е дистрибуирана близу до средната вредност. Големата варијанса покажува дека случајната променлива е дистрибуирана далеку од средната вредност. На пример, со нормална дистрибуција, тесната крива на bвончето ќе има мала варијанса и широката крива на ellвончето ќе има голема варијанса.

Дефиниција на варијанса

Варијансата на случајна променлива X е очекуваната вредност на квадратите на разликата од X и очекуваната вредност μ.

σ ² = Var ( X ) = E [( X - μ ) ² ]

Од дефиницијата за варијансата што можеме да ја добиеме

σ ² = Var ( X ) = E ( X ² ) - μ ²

Варијанса на континуирана случајна променлива

За континуирана случајна променлива со просечна вредност μ и функција на густина на веројатност f (x):

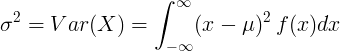
$\ сигма ^ 2 = Var (X) = \ int _ {- \ неправилен} ^ {\ неправилен} (x- \ mu) ^ 2 \: f (x) dx$

или

$Var (X) = \ лево [\ int _ {- \ неправилно} ^ {\ неправилно} x ^ 2 \: f (x) dx \ десно] - \ mu ^ 2$

Варијанса на дискретна случајна променлива

За дискретна случајна променлива X со средна вредност μ и функција на маса на веројатност P (x):

$\ сигма ^ 2 = Var (X) = \ sum_ {i} ^ {} (x_i- \ mu _X) ^ 2P_X (x_i)$

или

$Var (X) = \ лево [\ sum_ {i} ^ {} x_i ^ 2P (x_i) \ десно] - \ mu ^ 2$

Карактеристики на варијанса

Кога X и Y се независни случајни променливи:

Var ( X + Y ) = Var ( X ) + Var ( Y )

Стандардно отстапување

Варијанса

Дефиниција на варијанса

Варијанса на континуирана случајна променлива

Варијанса на дискретна случајна променлива

Карактеристики на варијанса

Var ( X + Y ) = Var ( X ) + Var ( Y )

Исто така види

ВЕBAНОСТ И СТАТИСТИКА

БРЗИ ТАБЕЛИ