Дистрибуција на веројатност

Според веројатноста и статистичката дистрибуција е карактеристика на случајна променлива, ја опишува веројатноста на случајната променлива во секоја вредност.

Секоја дистрибуција има одредена функција на густина на веројатност и функција на дистрибуција на веројатност.

Иако има неопределен број на дистрибуции на веројатност, постојат неколку вообичаени дистрибуции во употреба.

Функција на кумулативна дистрибуција

Распределбата на веројатноста е опишана со кумулативната функција на дистрибуција F (x),

што е веројатност случајната променлива X да добие вредност помала или еднаква на x:

F ( x ) = P ( X ≤ x )

Континуирана дистрибуција

Кумулативната функција на дистрибуција F (x) се пресметува со интеграција на функцијата густина на веројатност f (u) на континуирана случајна променлива X.

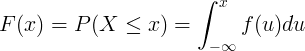
Дискретна дистрибуција

Кумулативната функција на дистрибуција F (x) се пресметува со збир на функцијата за маса на веројатност P (u) на дискретна случајна променлива X.

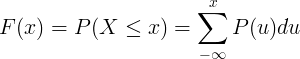
Табела за континуирани дистрибуции

Континуирана дистрибуција е дистрибуција на континуирана случајна променлива.

Пример за континуирана дистрибуција

...

Табела за континуирани дистрибуции

Име на дистрибуција Дистрибутивен симбол Функција на густина на веројатност (pdf) Средна Варијанса
   

f X ( x )

μ = E ( X )

σ 2 = Var ( X )
Нормално / гаусово

X ~ N (μ, σ 2 )

 \ frac {1} {\ sigma \ sqrt {2 \ pi}} e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ сигма ^ 2}} μ σ 2
Униформа

X ~ U ( a , b )

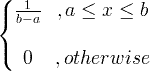 \ започнете со {Bmatrix} \ frac {1} {ba} &, a \ leq x \ leq b \\ & \\ 0 &, во спротивно \ end {матрица} \ frac {(ba) ^ 2} {12}
Експоненцијална X ~ екс (λ) \ започнете {Bmatrix} \ lambda e ^ {- \ lambda x} & x \ geq 0 \\ 0 & x <0 \ end {матрица} \ frac {1} {\ lambda} \ frac {1} {\ lambda ^ 2}
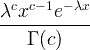Гама X ~ гама ( c , λ) \ frac {\ lambda ^ cx ^ {c-1} e ^ {- \ lambda x}} {\ Gamma (c)}

x / 0, c / 0, λ/ 0

 \ frac {c} {\ lambda} \ frac {c} {\ lambda ^ 2}
Плоштад Чи

X ~ χ 2 ( к )

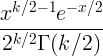 \ frac {x ^ {k / 2-1} e ^ {- x / 2}} {2 ^ {k / 2} \ Гама (k / 2)}

к

2 к
Вишарт        
F

X ~ F ( k 1 , k 2 )

      
Бета        
Вејбул        
Нормално

X ~ LN (μ, σ 2 )

      
Рејли        
Коши        
Дирихле        
Лаплас        
Леви        
Ориз        
Студентски т        

Табела за дискретни дистрибуции

Дискретна дистрибуција е дистрибуција на дискретна случајна променлива.

Пример за дискретна дистрибуција

...

Табела за дискретни дистрибуции

Име на дистрибуција Дистрибутивен симбол Функција на маса на веројатност (pmf) Средна Варијанса
    f x ( k ) = P ( X = k )

k = 0,1,2, ...

 Е ( x ) Var ( x )
Бином

X ~ корпа ( n , стр )

 \ binom {n} {k} p ^ {k} (1-p) ^ {nk}

np

np (1- p )
Поасон

X ~ Поасон (λ)

λ ≥ 0

λ

λ

Униформа

X ~ U ( a, b )

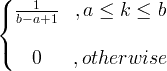 \ започнете со {Bmatrix} \ frac {1} {b-a + 1} &, a \ leq k \ leq b \\ & \\ 0 &, во спротивно \ end {матрица} \ frac {a + b} {2} \ frac {(b-a + 1) ^ {2} -1} {12}
Геометриски

X ~ Геом ( стр )

 p (1-p) ^ {k}

\ frac {1-p} {p}

\ frac {1-p} {p ^ 2}
Хипер-геометриски

X ~ HG ( N , K , n )

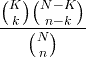N = 0,1,2, ...

K = 0,1, .., Н.

n = 0,1, ..., Н.

 \ frac {nK} {N} \ frac {nK (NK) (Nn)} {N ^ 2 (N-1)}
Бернули

X ~ Берн ( стр )

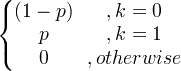 \ започнете {Bmatrix} (1-p) &, k = 0 \\ p &, k = 1 \\ 0 &, во спротивно \ end {матрица}

стр.

стр (1- стр )

 

Исто така види

Advertising

ВЕBAНОСТ И СТАТИСТИКА
БРЗИ ТАБЕЛИ