Líkindadreifing
Í líkindum og tölfræði er dreifing einkenni handahófsbreytu, lýsir líkum handahófskenndrar breytu í hverju gildi.
Hver dreifing hefur ákveðna möguleika á þéttleika og líkindadreifingu.
Þó að það sé óákveðinn fjöldi líkindadreifinga eru nokkrar algengar dreifingar í notkun.
Uppsöfnuð dreifingaraðgerð
Líkindadreifingunni er lýst með uppsöfnuðum dreifingaraðgerð F (x),
sem eru líkurnar á að handahófsbreytan X fái gildi sem er minna en eða jafnt og x:
F ( x ) = P ( X ≤ x )
Stöðug dreifing
Uppsöfnuð dreifingaraðgerð F (x) er reiknuð með samþættingu líkindaþéttleikafallsins f (u) samfelldrar handahófsbreytu X.
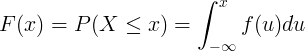
Stakur dreifing
Uppsöfnuð dreifingarfall F (x) er reiknað með samantekt líkindamassafallsins P (u) stakrar handahófsbreytu X.
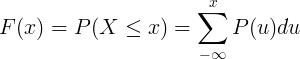
Stöðug dreifingartafla
Stöðug dreifing er dreifing samfelldrar handahófsbreytu.
Stöðugt dreifingardæmi
...
Stöðug dreifingartafla
| Dreifingarheiti | Dreifingartákn | Líkindi þéttleika virka (pdf) | Vondur | Afbrigði |
|---|---|---|---|---|
|
f X ( x ) |
μ = E ( X ) |
σ 2 = Var ( X ) |
||
| Venjulegur / gaussískur |
X ~ N (μ, σ 2 ) |
|
μ | σ 2 |
| Einkennisbúningur |
X ~ U ( a , b ) |
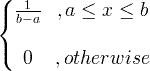 |
|
|
| Veldisvísir | X ~ exp (λ) |
|
|
|
| Gamma | X ~ gamma ( c , λ) |
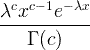 x / 0, c / 0, λ/ 0 |
|
|
| Chi ferningur |
X ~ χ 2 ( k ) |
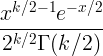 |
k |
2 k |
| Wishart | ||||
| F |
X ~ F ( k 1 , k 2 ) |
|||
| Beta | ||||
| Weibull | ||||
| Log-normal |
X ~ LN (μ, σ 2 ) |
|||
| Rayleigh | ||||
| Cauchy | ||||
| Dirichlet | ||||
| Laplace | ||||
| Álagning | ||||
| Hrísgrjón | ||||
| Nemandi t |
Sérstök dreifingartafla
Stakur dreifing er dreifing stakrar handahófsbreytu.
Dæmi um dreifða dreifingu
...
Sérstök dreifingartafla
| Dreifingarheiti | Dreifingartákn | Líkur á massafalli (pmf) | Vondur | Afbrigði | |
|---|---|---|---|---|---|
|
f x ( k ) = P ( X = k ) k = 0,1,2, ... |
E ( x ) | Var ( x ) | |||
| Tvíliða |
X ~ rusl ( n , p ) |
|
np |
np (1- p ) |
|
| Poisson |
X ~ Poisson (λ) |
|
λ ≥ 0 |
λ |
λ |
| Einkennisbúningur |
X ~ U ( a, b ) |
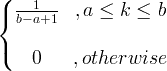 |
|
|
|
| Geometric |
X ~ Geom ( p ) |
|
|
|
|
| Há-rúmfræðilegt |
X ~ HG ( N , K , n ) |
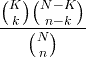 |
N = 0,1,2, ... K = 0,1, .., N n = 0,1, ..., N |
|
|
| Bernoulli |
X ~ Bern ( p ) |
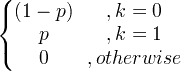 |
p |
p (1- p ) |
|
Sjá einnig
Advertising
Líkindi og tölfræði
HRAÐ TÖFLUR