Logarithm reglur

The undirstaða b Logri af mörgum er veldisvísirinn sem við þurfum að hækka grunn til þess að fá númerið.

Logarithm skilgreining

Þegar b er hækkað í krafti y er jafnt x:

b y = x

Þá er grunnb lógaritmi x jafn y:

log b ( x ) = y

Til dæmis þegar:

2 4 = 16

Þá

log 2 (16) = 4

Lógaritmi sem andhverft fall veldisfallsins

Lógaritmíska aðgerðin,

y = log b ( x )

er andhverfa fall veldisfallsins,

x = b y

Þannig að ef við reiknum út veldisfall lógaritmans x (x/ 0),

f ( f -1 ( x )) = b log b ( x ) = x

Eða ef við reiknum út lógaritm af veldisfalli x,

f -1 ( f ( x )) = log b ( b x ) = x

Náttúrulegur lógaritmi (ln)

Náttúrulegur lógaritmi er lógaritmi við grunninn e:

ln ( x ) = log e ( x )

Þegar e fasti er talan:

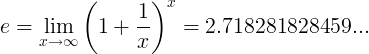
e = \ lim_ {x \ rightarrow \ infty} \ left (1+ \ frac {1} {x} \ right) ^ x = 2.718281828459 ...

eða

e = \ lim_ {x \ rightarrow 0} \ left (1+ \ right x) ^ \ frac {1} {x}

 

Sjá: Náttúrulegur lógaritmi

Andhverfur lógaritmaútreikningur

Andhverfur lógaritmi (eða andstæðingur lógaritmi) er reiknaður með því að hækka grunninn b að lógaritmanum y:

x = log -1 ( y ) = b y

Logarithmic virka

Lógaritmíska aðgerðin hefur grunnformið af:

f ( x ) = log b ( x )

Logarithm reglur

Regluheiti Regla
Vöruregla lógaritma
 log b ( x ∙ y ) = log b ( x ) + log b ( y )
Regla um lógaritma
 log b ( x / y ) = log b ( x ) - log b ( y )
Völdregla lógaritma
 log b ( x y ) = y ∙ log b ( x )
Logarithm grunnrofaregla
 log b ( c ) = 1 / log c ( b )
Breytingarregla um lógaritma
 log b ( x ) = log c ( x ) / log c ( b )
Afleiða lógaritma
 f ( x ) = log b ( x ) ⇒ f ' ( x ) = 1 / ( x ln ( b ))
Óaðskiljanlegur lógaritmi
 ∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C
Logaritmi neikvæðrar tölu
 log b ( x ) er óskilgreint þegar x ≤ 0
Logaritmi 0
 log b (0) er óskilgreint
\ lim_ {x \ til 0 ^ +} \ textup {log} _b (x) = - \ infty
Logarithm af 1
 log b (1) = 0
Logaritmi grunnsins
 log b ( b ) = 1
Logaritmi óendanleikans
 lim log b ( x ) = ∞, þegar x → ∞

Sjá: Logarithm reglur

 

Vöruregla lógaritma

Lógaritmi margföldunar x og y er summan lógaritma x og lógaritma y.

log b ( x ∙ y ) = log b ( x ) + log b ( y )

Til dæmis:

log 10 (3 ∙ 7) = log 10 (3) + log 10 (7)

Regla um lógaritma

Lógaritmi deilingar x og y er mismunur lógaritma x og lógaritma y.

log b ( x / y ) = log b ( x ) - log b ( y )

Til dæmis:

skrá sig inn 10 (3 / 7) = log 10. (3) - skrá sig inn 10 (7)

Völdregla lógaritma

Lógaritmi x hækkaður í krafti y er y sinnum lógaritmi x.

log b ( x y ) = y ∙ log b ( x )

Til dæmis:

log 10 (2 8 ) = 8 ∙ log 10 (2)

Logarithm grunnrofaregla

Grunn b lógaritma c er 1 deilt með grunn c lógaritma b.

log b ( c ) = 1 / log c ( b )

Til dæmis:

log 2 (8) = 1 / log 8 (2)

Breytingarregla um lógaritma

Grunn b lógaritma x er grunn c lógaritmi x deilt með grunn c lógaritma b.

log b ( x ) = log c ( x ) / log c ( b )

Til dæmis, til þess að reikna út log 2 (8) í reiknivél, verðum við að breyta grunninum í 10:

log 2 (8) = log 10 (8) / log 10 (2)

Sjá: regla um breytingu á grunnbók

Logaritmi neikvæðrar tölu

Grunnurinn b raunverulegur lógaritmi x þegar x <= 0 er óskilgreindur þegar x er neikvæður eða jafn núll:

log b ( x ) er óskilgreint þegar x ≤ 0

Sjá: log yfir neikvæða tölu

Logaritmi 0

Grunn b lógaritmi núlls er óskilgreindur:

log b (0) er óskilgreint

Mörk grunn b lógaritma x, þegar x nálgast núll, eru mínus óendanleiki:

\ lim_ {x \ til 0 ^ +} \ textup {log} _b (x) = - \ infty

Sjá: log af núlli

Logarithm af 1

Grunn b lógaritmi eins er núll:

log b (1) = 0

Til dæmis er grunnur tveggja lógaritma af einum núll:

log 2 (1) = 0

Sjá: log af einum

Logaritmi óendanleikans

Mörk grunn b lógaritma x, þegar x nálgast óendanleikann, eru jöfn óendanleikanum:

lim log b ( x ) = ∞, þegar x → ∞

Sjá: log of infinity

Logaritmi grunnsins

Grunn b lógaritma b er einn:

log b ( b ) = 1

Til dæmis er grunnur tveggja lógaritma af tveimur einn:

log 2 (2) = 1

Lógaritmaafleiða

Hvenær

f ( x ) = log b ( x )

Síðan afleiða f (x):

f ' ( x ) = 1 / ( x ln ( b ))

Sjá: log afleiða

Logarithm óaðskiljanlegur

Heildarþáttur lógaritma x:

∫ log b ( x ) dx = x ∙ (log b ( x ) - 1 / ln ( b ) ) + C

Til dæmis:

∫ log 2 ( x ) dx = x ∙ (log 2 ( x ) - 1 / ln (2) ) + C

Logarithm nálgun

log 2 ( x ) ≈ n + ( x / 2 n - 1),

Flókinn lógaritmi

Fyrir flókið númer z:

z = re iθ = x + iy

Flókinn lógaritmi verður (n = ...- 2, -1,0,1,2, ...):

Log z = ln ( r ) + i ( θ + 2nπ ) = ln (√ ( x 2 + y 2 )) + i · arctan ( y / x ))

Logarithm vandamál og svör

Dæmi # 1

Finndu x fyrir

log 2 ( x ) + log 2 ( x -3) = 2

Lausn:

Notkun vörureglunnar:

log 2 ( x ∙ ( x -3)) = 2

Að breyta lógaritmaforminu samkvæmt skilgreiningu lógaritma:

x ∙ ( x -3) = 2 2

Eða

x 2 -3 x -4 = 0

Leysa fjórða jöfnu:

x 1,2 = [3 ± √ (9 + 16)] / 2 = [3 ± 5] / 2 = 4, -1

Þar sem lógaritminn er ekki skilgreindur fyrir neikvæðar tölur er svarið:

x = 4

Dæmi # 2

Finndu x fyrir

log 3 ( x +2) - log 3 ( x ) = 2

Lausn:

Notaðu stuðulregluna:

log 3 (( x +2) / x ) = 2

Að breyta lógaritmaforminu samkvæmt skilgreiningu lógaritma:

( x +2) / x = 3 2

Eða

x +2 = 9 x

Eða

8 x = 2

Eða

x = 0,25

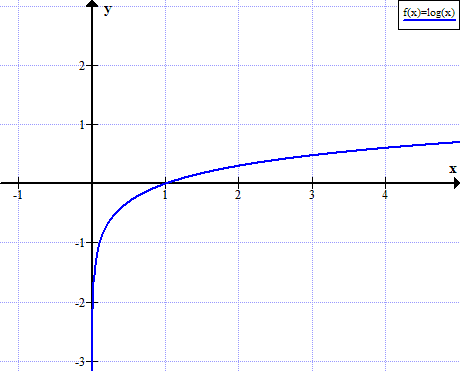
Graf af log (x)

log (x) er ekki skilgreint fyrir raunveruleg, ekki jákvæð gildi x:

Logarithms tafla

x log 10 x log 2 x log e x
0 óskilgreint óskilgreint óskilgreint
0 + - ∞ - ∞ - ∞
0.0001 -4 -13.287712 -9.210340
0,001 -3 -9.965784 -6.907755
0,01 -2 -6.643856 -4.605170
0,1 -1 -3.321928 -2.302585
1 0 0 0
2 0.301030 1 0.693147
3 0.477121 1.584963 1.098612
4 0,602060 2 1.386294
5 0.698970 2.321928 1.609438
6 0.778151 2.584963 1.791759
7 0.845098 2.807355 1.945910
8 0,903090 3 2.079442
9 0.954243 3.169925 2.197225
10 1 3.321928 2.302585
20 1.301030 4.321928 2.995732
30 1.477121 4.906891 3.401197
40 1.602060 5.321928 3.688879
50 1.698970 5.643856 3.912023
60 1.778151 5.906991 4.094345
70 1.845098 6.129283 4.248495
80 1.903090 6.321928 4.382027
90 1.954243 6.491853 4.499810
100 2 6.643856 4.605170
200 2.301030 7.643856 5.298317
300 2.477121 8.228819 5.703782
400 2.602060 8.643856 5.991465
500 2.698970 8.965784 6.214608
600 2.778151 9.228819 6.396930
700 2.845098 9.451211 6.551080
800 2.903090 9.643856 6.684612
900 2.954243 9.813781 6.802395
1000 3 9.965784 6.907755
10000 4 13.287712 9.210340

 

Logarithm reiknivél ►

 

Sjá einnig

Advertising

ALGEBRA
HRAÐ TÖFLUR